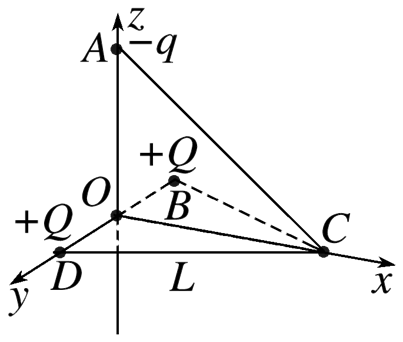
如图所示,水平面内的等边三角形 $B C D$ 的边长为 $L, C$ 点恰好位于光滑绝缘直轨道 $A C$ 的最低点,$A$ 点到 $B 、 D$ 两点的距离均为 $L, A$ 点在 $B D$ 边上的坚直投影点为 $O . y$ 轴上 $B 、 D$ 两点固定两个电荷量均为 $Q$ 的正点电荷.在 $A$ 点将质量为 $m$ 、电荷量为 $-q$ 的小球(自身产生的电场可忽略)套在轨道 $A C$ 上并将小球由静止释放,已知静电力常量为 $k$ ,重力加速度为 $g$ ,且 $k \frac{Q q}{L^2}=\frac{\sqrt{3}}{3} m g$ ,忽略空气阻力,下列说法正确的是
A
从 $O$ 点沿 $z$ 轴到 $A$ 点,电场强度一直增大
B
轨道上 $C$ 点的电场强度大小为 $\frac{m g}{q}$
C
小球刚到达 $C$ 点时(未脱离轨道)的加速度大小为 $\sqrt{3} g$
D
小球在 $A 、 C$ 两点之间做往复运动
E
F