单选题 （共 11 题 ），每题只有一个选项正确
甲、乙两带电小球的质量均为m，所带电荷量分别为＋q和－q，两球间用绝缘细线2连接，甲球用绝缘细线1悬挂在天花板上，在两球所在空间有沿水平方向向左的匀强电场，电场强度大小为E，且有qE＝mg，g为重力加速度，平衡时细线都被拉直.则平衡时的可能位置是
$\text{A.}$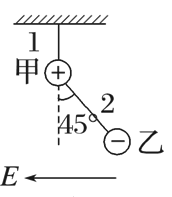 
$\text{B.}$ 
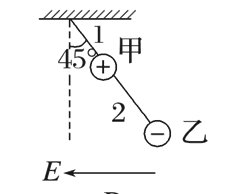$\text{C.}$ 
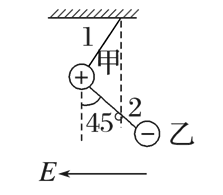$\text{D.}$ 
如图所示，水平地面上固定一竖直的光滑绝缘细杆，一质量为m、带电荷量为q的圆环a套在竖直杆上，质量为M、带电荷量为＋Q的滑块b静置于水平地面上，滑块b与地面间的动摩擦因数为μ，a、b均保持静止，且两者连线与水平地面的夹角为θ，静电力常量为k，重力加速度为g，下列说法正确的是
$\text{A.}$ 圆环a带负电
$\text{B.}$ 滑块b受到的库仑力大小为 mg/cos $\theta$
$\text{C.}$ 滑块b受到地面的支持力大小为(M＋m)g
$\text{D.}$ 滑块b受到地面的摩擦力大小为μ(M＋m)g
带有等量异种电荷的一对平行金属板，如果两极板间距不是足够近或者两极板面积不是足够大，即使在两极板之间，它的电场线也不是彼此平行的直线，而是如图所示的曲线，关于这种电场，以下说法正确的是
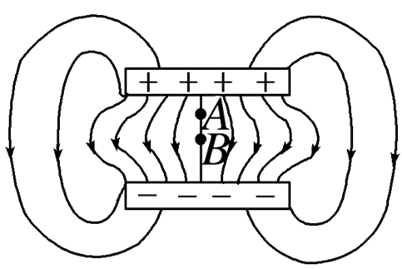
$\text{A.}$ 这种电场的电场线虽然是曲线，但是电场线的分布却是左右对称的， 很有规律性，它们之间的电场，除边缘部分外，可以看成匀强电场
$\text{B.}$ 电场内部A点的电场强度小于B点的电场强度
$\text{C.}$ 电场内部A点的电场强度等于B点的电场强度
$\text{D.}$ 若将一正电荷从电场中的A点由静止释放， 它将沿着电场线方向运动到负极板
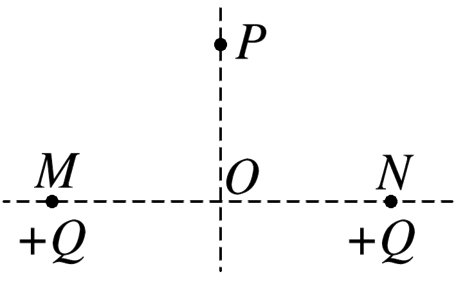
如图所示，M、N为两个等量同种正点电荷，在其连线的中垂线上的P点自由释放一点电荷q，不计重力，下列说法中正确的是
$\text{A.}$ 点电荷一定会向O运动，加速度一定越来越大，速度也一定越来越大
$\text{B.}$ 点电荷可能会向O运动，加速度一定越来越小，速度一定越来越大
$\text{C.}$ 若点电荷能越过O点，则一定能运动到P关于O的对称点且速度再次为零
$\text{D.}$ 若点电荷能运动到O点，此时加速度达到最大值，速度为零
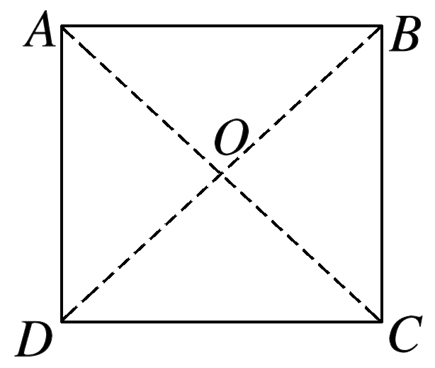
如图所示，正方形ABCD四个顶点各固定一个带正电的点电荷，电荷量相等，O是正方形的中心，将A点的电荷沿OA的延长线向无穷远处移动，则
$\text{A.}$ 在移动过程中，O点电场强度变小
$\text{B.}$ 在移动过程中，C点的电荷所受静电力变大
$\text{C.}$ 在移动过程中，移动的电荷所受静电力做负功
$\text{D.}$ 当其移动到无穷远处时，O点的电势高于A点
如图所示，两个固定的半径均为r的细圆环同轴放置，O1、O2分别为两细圆环的圆心，且O1O2＝2r，两圆环分别带有均匀分布的等量异种电荷＋Q、－Q(Q>0).一带正电的粒子(重力不计)从O1由静止释放.静电力常量为k.下列说法正确的是
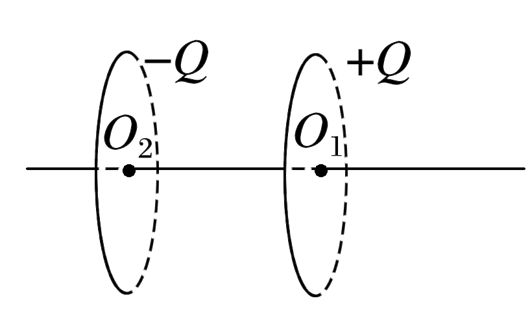
$\text{A.}$ O1O2的电场强调为 $\frac{\sqrt{2}kQ}{2r^2}$
$\text{B.}$ O1O2的电场强调为 $\frac{\sqrt{2}kQ}{4r^2}$
$\text{C.}$ 粒子在O1O2中点处动能最大
$\text{D.}$ 粒子在O2处动能最大
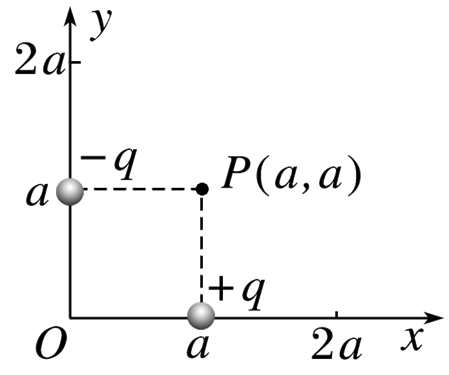
如图，在 $(a, 0)$ 位置放置电荷量为 $q$ 的正点电荷，在 $(0, a)$位置放置电荷量为 $q$ 的负点电荷，在距 $P(a, a)$ 为 $\sqrt{2} a$ 的某点处放置正点电荷 $Q$ ，使得 $P$ 点的电场强度为零．则 $Q$ 的位置及电荷量分别为
$\text{A.}$ $(0,2 a), \sqrt{2} q$
$\text{B.}$ $(0,2 a), 2 \sqrt{2} q$
$\text{C.}$ $(2 a, 0), \sqrt{2} q$
$\text{D.}$ $(2 a, 0), \quad 2 \sqrt{2} q$
如图所示，水平面内的等边三角形 $B C D$ 的边长为 $L, C$ 点恰好位于光滑绝缘直轨道 $A C$ 的最低点，$A$ 点到 $B 、 D$ 两点的距离均为 $L, A$ 点在 $B D$ 边上的坚直投影点为 $O . y$ 轴上 $B 、 D$ 两点固定两个电荷量均为 $Q$ 的正点电荷．在 $A$ 点将质量为 $m$ 、电荷量为 $-q$ 的小球（自身产生的电场可忽略）套在轨道 $A C$ 上并将小球由静止释放，已知静电力常量为 $k$ ，重力加速度为 $g$ ，且 $k \frac{Q q}{L^2}=\frac{\sqrt{3}}{3} m g$ ，忽略空气阻力，下列说法正确的是
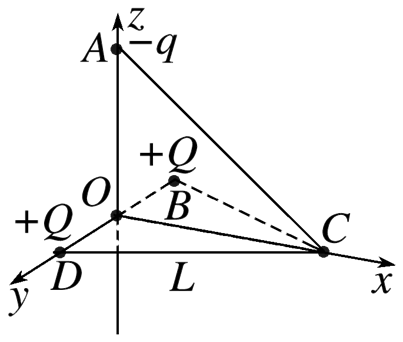
$\text{A.}$ 从 $O$ 点沿 $z$ 轴到 $A$ 点，电场强度一直增大
$\text{B.}$ 轨道上 $C$ 点的电场强度大小为 $\frac{m g}{q}$
$\text{C.}$ 小球刚到达 $C$ 点时（未脱离轨道）的加速度大小为 $\sqrt{3} g$
$\text{D.}$ 小球在 $A 、 C$ 两点之间做往复运动
如图所示，不带电的金属球N的半径为R，球心为O，球N左侧固定着两个电荷量大小均为q的异种点电荷，电荷之间的距离为2R.M点在点电荷＋q的右侧R处，M点和O点以及＋q、－q所在位置在同一直线上，且两点电荷连线的中点到O点的距离为5R.当金属球达到静电平衡时，下列说法正确的是
$\text{A.}$ M点的电势低于O点的电势
$\text{B.}$ $M$ 点的电场强度大小为 $\frac{8 k q}{9 R^2}$
$\text{C.}$ 感应电荷在球心 $O$ 处产生的电场强度大小为 $\frac{5 k q}{144 R^2}$
$\text{D.}$ 将一电子由 $M$ 点移到金属球上不同点，克服静电力所做的功不相等
如图所示，真空中有一电荷均匀分布的带正电圆环，半径为 $r$ ，带电荷量为 $q$ ，圆心 $O$ 在 $x$ 轴的坐标原点处，圆环的边缘 $A$ 点与 $x$ 轴上 $P$ 点的连线与 $x$ 轴的夹角为 $37^{\circ}$ ，静电力常量为 $k$ ，取 $\sin 37^{\circ}=\frac{3}{5}, \cos 37^{\circ}=\frac{4}{5}$ ，则整个圆环产生的电场在 $P$ 点的电场强度大小为
$\text{A.}$ $\frac{27 k q}{125 r^2}$
$\text{B.}$ $\frac{36 k q}{125 r^2}$
$\text{C.}$ $\frac{48 k q}{125 r^2}$
$\text{D.}$ $\frac{64 k q}{125 r^2}$
如图所示，电荷均匀分布在半球面上，它在这半球的中心 $O$ 处电场强度大小等于 $E_0$ ，两个通过同一条直径的平面夹角为 $\alpha$ ，从半球中分出夹角为 $\alpha$ 的这部分球面，则所分出的这部分球面上（在＂小瓣＂上）的电荷在 $O$处的电场强度大小为
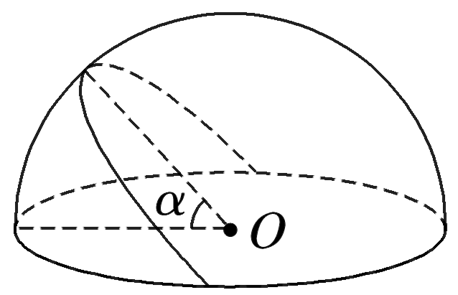
$\text{A.}$ $E=E_0 \sin \alpha$
$\text{B.}$ $E=E_0 \cos \alpha$
$\text{C.}$ $E=E_0 \cos \frac{\alpha}{2}$
$\text{D.}$ $E=E_0 \sin \frac{\alpha}{2}$
多选题 （共 2 题 ），每题有多个选项正确
$M$ 和 $N$ 是两个不带电的物体．它们互相摩擦后 $M$ 带正电且所带电荷量为 $1.6 \times 10^{-10} C$ ，下列判断正确的有
$\text{A.}$ 摩擦前 $M$ 和 $N$ 的内部没有任何电荷
$\text{B.}$ 摩擦过程中电子从 $M$ 转移到 $N$
$\text{C.}$ $N$ 在摩擦后一定带负电且所带电荷量为 $1.6 \times 10^{-10} C$
$\text{D.}$ $M$ 在摩擦过程中失去 $1.6 \times 10^{10}$ 个电子
如图，三个点电荷A、B、C分别位于等边三角形的顶点上，A、B都带正电荷，A所受B、C两个电荷的静电力的合力如图中FA所示，已知FA与BA延长线的夹角小于60°，则对点电荷C所带电荷的电性和电荷量的判断正确的是
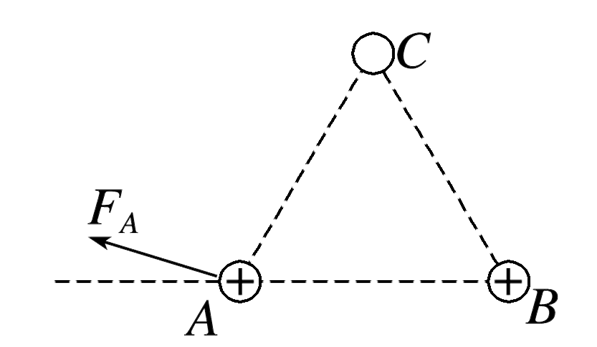
$\text{A.}$ 一定是正电
$\text{B.}$ 一定是负电
$\text{C.}$ 带电荷量大于B的
$\text{D.}$ 带电荷量小于B的