如图所示，处于坚直平面内的一探究装置，由倾角 $\alpha=37^{\circ}$ 的光滑直轨道 $A B$ ，圆心为 $O_1$ 的半圆形光滑轨道 $B C D$ ，圆心为 $O_2$ 的半圆形光滑细圆管轨道 $D E F$ ，倾角也为 $37^{\circ}$ 的粗糙直轨道 $F G$ 组成， $B, ~ D$ 和 $F$ 为轨道间的相切点，弹性板垂直轨道固定在 $G$ 点（与 $B$ 点等高）， $B, ~ O_1, ~ D, ~ O_2$ 和 $F$ 点处于同一直线上．已知可视为质点的滑块质量 $m=0.1$ kg ，轨道 $B C D$ 和 $D E F$ 的半径 $R=0.15 m$ ，轨道 $A B$ 长度 $l_{A B}=3 m$ ，滑块与轨道 $F G$ 间的动摩擦因数 $\mu=\frac{7}{8}$ ，滑块与弹性板作用后，以等大速度弹回， $\sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$ ．滑块开始时均从轨道 $A B$ 上某点静止释放．


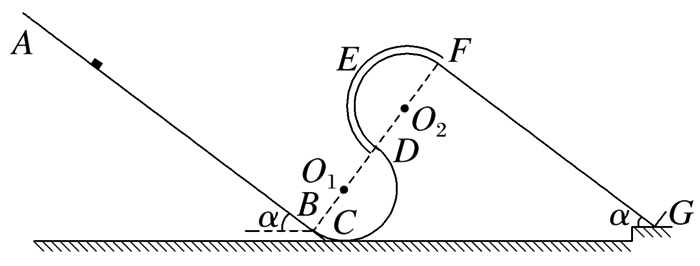
(1)若释放点距B点的长度l＝0.7 m，求滑块到最低点C时轨道对其支持力FN的大小；

(2)设释放点距B点的长度为lx，求滑块第一次经F点时的速度v与lx之间的关系式；

(3)若滑块最终静止在轨道FG的中点，求释放点距B点长度lx的值.