单选题 (共 3 题 ),每题只有一个选项正确
如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC水平,其长度d=0.50 m,盆边缘的高度为h=0.30 m.在A处放一个质量为m的小物块并让其由静止下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.1.小物块在盆内来回滑动,最后停下来,则停止的地点到B的距离为

$\text{A.}$ 0.50 m
$\text{B.}$ 0.25 m
$\text{C.}$ 0.10 m
$\text{D.}$ 0
如图所示,一物体由固定斜面上的A点以初速度v0下滑到底端B,它与挡板发生无动能损失的碰撞后又滑回到A点,其速度恰好为零.设A、B两点高度差为h,重力加速度为g,则它与挡板碰前瞬间的速度大小为
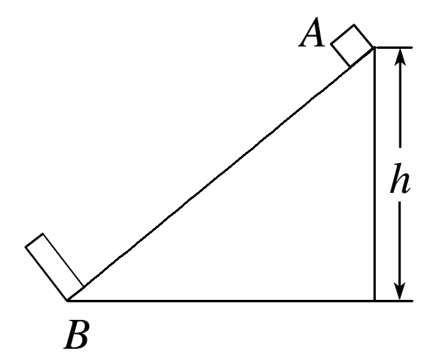
$\text{A.}$ $\sqrt{2 g h+\frac{v_0^2}{4}}$
$\text{B.}$ $\sqrt{2 g h}$
$\text{C.}$ $\sqrt{2 g h+\frac{v_0{ }^2}{2}}$
$\text{D.}$ $\sqrt{2 g h+v_0{ }^2}$
如图所示,两倾角均为θ的光滑斜面对接后固定在水平地面上,O点为斜面的最低点.一个小物块从右侧斜面上高为H处由静止滑下,在两个斜面上做往复运动.小物块每次通过O点时都会有动能损失,损失的动能为小物块当次到达O点时动能的5%.小物块从开始下滑到停止的过程中运动的总路程为

$\text{A.}$ $ \cdot \frac{49 H}{\sin \theta}$
$\text{B.}$ $\frac{39 H}{\sin \theta}$
$\text{C.}$ $\frac{29 H}{\sin \theta}$
$\text{D.}$ $\frac{20 H}{\sin \theta}$
多选题 (共 1 题 ),每题有多个选项正确
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后将以原速率返回.现将滑块拉到A点由静止释放,与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,由此可以确定

$\text{A.}$ 滑块下滑和上滑过程加速度大小a1、a2
$\text{B.}$ 滑块第1次与挡板碰撞前的速度v1
$\text{C.}$ 滑块与杆之间的动摩擦因数μ
$\text{D.}$ 滑块第k次与挡板碰撞到第k+1次与挡板碰撞的时间间隔Δt
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示,处于坚直平面内的一探究装置,由倾角 $\alpha=37^{\circ}$ 的光滑直轨道 $A B$ ,圆心为 $O_1$ 的半圆形光滑轨道 $B C D$ ,圆心为 $O_2$ 的半圆形光滑细圆管轨道 $D E F$ ,倾角也为 $37^{\circ}$ 的粗糙直轨道 $F G$ 组成, $B, ~ D$ 和 $F$ 为轨道间的相切点,弹性板垂直轨道固定在 $G$ 点(与 $B$ 点等高), $B, ~ O_1, ~ D, ~ O_2$ 和 $F$ 点处于同一直线上.已知可视为质点的滑块质量 $m=0.1$ kg ,轨道 $B C D$ 和 $D E F$ 的半径 $R=0.15 m$ ,轨道 $A B$ 长度 $l_{A B}=3 m$ ,滑块与轨道 $F G$ 间的动摩擦因数 $\mu=\frac{7}{8}$ ,滑块与弹性板作用后,以等大速度弹回, $\sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$ .滑块开始时均从轨道 $A B$ 上某点静止释放.
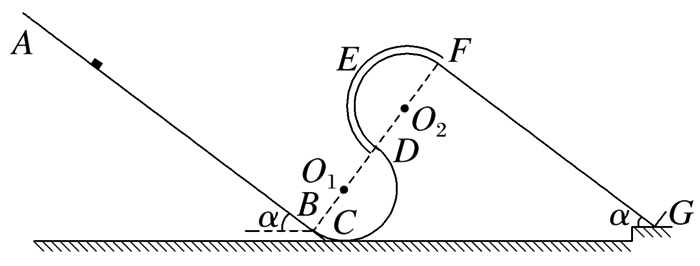
(1)若释放点距B点的长度l=0.7 m,求滑块到最低点C时轨道对其支持力FN的大小;
(2)设释放点距B点的长度为lx,求滑块第一次经F点时的速度v与lx之间的关系式;
(3)若滑块最终静止在轨道FG的中点,求释放点距B点长度lx的值.
如图所示,倾角为θ=37°的足够长光滑固定斜面AB与长LBC=2 m的粗糙水平面BC用一小段光滑圆弧(长度不计,未画出)平滑连接,半径R=1.5 m的光滑圆弧轨道CD与水平面相切于C点,OD与水平方向的夹角也为θ=37°.质量为m的小滑块从斜面上距B点L0=2 m的位置由静止开始下滑,恰好运动到C点.已知重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
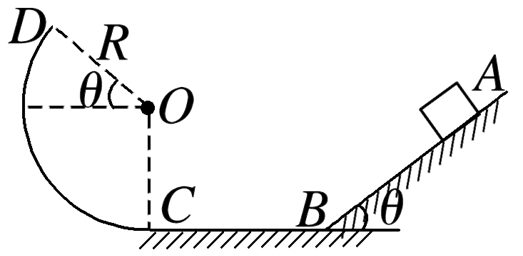
(1)求小滑块与粗糙水平面BC间的动摩擦因数μ;
(2)改变小滑块从斜面上开始释放的位置,使小滑块能够通过D点,求小滑块的释放位置与B点的最小距离.
一篮球质量为m=0.60 kg,一运动员使其从距地面高度为h1=1.8 m处由静止自由落下,反弹高度为h2=1.2 m.若使篮球从距地面h3=1.5 m的高度由静止下落,并在开始下落的同时向下拍球、球落地后反弹的高度也为1.5 m.假设运动员拍球时对球的作用力为恒力,作用时间为t=0.20 s;该篮球每次与地面碰撞前后的动能的比值不变.重力加速度大小取g=10 m/s2,不计空气阻力.求:
(1)运动员拍球过程中对篮球所做的功;
(2)运动员拍球时对篮球的作用力的大小.
如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达A孔进入半径R=0.3 m的固定在水平面上竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2 m,θ=53°,小球质量为m=0.5 kg,D点与A孔的水平距离s=2 m,g取10 m/s2.(sin 53°=0.8,cos 53°=0.6)
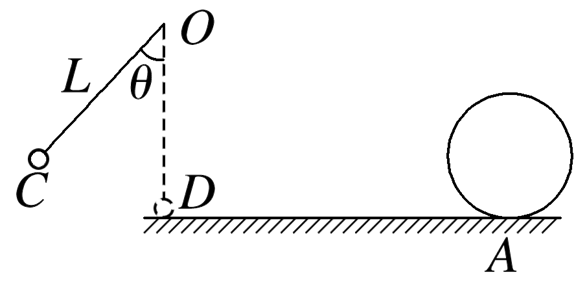
(1)求摆线能承受的最大拉力为多大;
(2)要使摆球能进入圆轨道并且不脱离轨道,求摆球与粗糙水平面间的动摩擦因数μ的范围.