数学

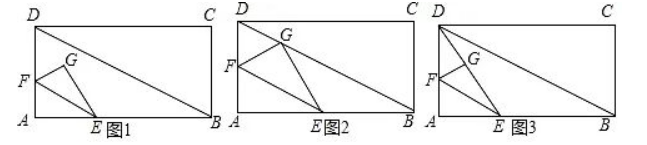
如图1，矩形 $A B C D$ 中, $A B=8, B C=6$, 点 $E, F$ 分别为 $A B, A D$ 边上任意一点, 现将 $\triangle A E F$ 沿直线 $E F$ 对折，点 $A$ 对应点为点 $G$.
(1) 如图2, 当 $E F // B D$, 且点 $G$ 落在对角线 $B D$ 上时, 求 $D G$ 的长;
(2) 如图3, 连接 $D G$, 当 $E F// B D$ 且 $\triangle D F G$ 是直角三角形时, 求 $A E$ 的值;
(3) 当 $A E=2 A F$ 时, $F G$ 的延长线交 $\triangle B C D$ 的边于点 $H$, 是否存在一点 $H$, 使得以 $E, H, G$ 为顶点的三角 形与 $\triangle A E F$ 相似, 若存在, 请求出 $A E$ 的值; 若不存在, 请说明理由

已知曲线型构件 $L:\left\{\begin{array}{l}z=x^2+y^2, \\ x+y+z=1\end{array}\right.$ 的线密度为 $\rho=\left|x^2+x-y^2-y\right|$, 求 $L$ 的质量.