解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $p: x^2-7 x+10 < 0, q: x^2-4 m x+3 m^2 < 0$, 其中 $m>0$.
(1) 若 $m=4$, 且 $p \wedge q$ 为真, 求 $x$ 的取值范围;
(2) 若 $\neg q$ 是 $\neg p$ 的充分不必要条件, 求实数 $m$ 的取值范围.
已知抛物线 $y^2=2 p x(1 < p < 3)$ 的焦点为 $F$, 抛物线上的点 $M\left(x_0, 1\right)$ 到准线的距离为 $\frac{5}{4}$.
(1) 求抛物线的标准方程;
(2) 设直线 $M F$ 与抛物线的另一交点为 $N$, 求 $\frac{|M F|}{|N F|}$ 的值.
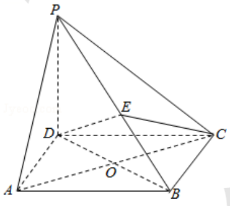
如图, 在四棱锥 $P-A B C D$ 中, $P D \perp$ 平面 $A B C D$, 四边形 $A B C D$ 是菱形, $A C=2, B D=2 \sqrt{3}$, 且 $A C, B D$ 交于点 $O, E$ 是 $P B$ 上任意一点.
(1) 求证: $A C \perp D E$;
(2) 若 $E$ 为 $P B$ 的中点, 且二面角 $A-P B-D$ 的余弦值为 $\frac{\sqrt{21}}{7}$, 求 $E C$与平面 $P A B$ 所成角 $\theta$ 的正弦值.