单选题 (共 5 题 ),每题只有一个选项正确
函数 $f(x)=\frac{1}{3} x^3+\frac{1}{2} x^2+6 x+1$ 的图形在点 $(0,1)$ 处的切线与 $x$ 轴交点的坐标是
$\text{A.}$ $\left(-\frac{1}{6}, 0\right)$
$\text{B.}$ $(-1,0)$
$\text{C.}$ $\left(\frac{1}{6}, 0\right)$
$\text{D.}$ $(1,0)$
若 $f(x)$ 与 $g(x)$ 在 $(-\infty, \infty)$ 上皆可导,且 $f(x) < g(x)$ ,则必有
$\text{A.}$ $f(-x)>g(-x)$
$\text{B.}$ $f^{\prime}(x) < g^{\prime}(x)$
$\text{C.}$ $\lim _{x \rightarrow x_0} f(x) < \lim _{x \rightarrow x_0} g(x)$
$\text{D.}$ $\int_0^x f(t) \mathrm{d} t < \int_0^x g(t) \mathrm{d} t$
若函数 $y=f(x)$ 有 $f^{\prime}\left(x_0\right)=\frac{1}{2}$ ,则 $\Delta x \rightarrow 0$ 时,该函数在 $x=x_0$ 处的微分 $\mathrm{d} y$ 是
$\text{A.}$ 与 $\Delta x$ 等价的无穷小
$\text{B.}$ 与 $\Delta x$ 同阶的无穷小
$\text{C.}$ 比 $\Delta x$ 低阶的无穷小
$\text{D.}$ 比 $\Delta x$ 高阶的无穷小
曲线 $y=\sin ^2 x(0 \leq x \leq \pi)$ 与 $x$ 轴围成的图形绕 $x$ 轴旋转所形成的旋转体体积为
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{4}{3} \pi$
$\text{C.}$ $\frac{2}{3} \pi^2$
$\text{D.}$ $\frac{2}{3} \pi$
$n$ 维向量组 $\alpha_1, \alpha_2, \cdots, \alpha_s(3 \leq s \leq n)$ 线性无关的充分必要条件是
$\text{A.}$ 存在一组不全为 0 的数 $k_1, k_2, \cdots, k_s$, 使 $ k_1 \alpha_1+k_2 \alpha_2+\cdots+k_s \alpha_s \neq 0 $
$\text{B.}$ $\alpha_1, \alpha_2, \cdots, \alpha_s$ 中任意两个向量都线性无关
$\text{C.}$ $\alpha_1, \alpha_2, \cdots, \alpha_s$ 中存在一个向量,它不能用其余向量线性表出
$\text{D.}$ $\alpha_1, \alpha_2, \cdots, \alpha_s$ 中任意一个向量都不能用其余向量线性表出
填空题 (共 5 题 ),请把答案直接填写在答题纸上
若 $f(x)=\left\{\begin{array}{ll}e^x(\sin x+\cos x), & x>0 \\ 2 x+\alpha, & x \leq 0\end{array}\right.$ 是 $(-\infty, \infty)$ 上的连续函数,则 $\alpha=$
若 $f(t)=\lim _{x \rightarrow \infty} t\left(1+\frac{1}{x}\right)^{2 t x}$, 则 $f^{\prime}(t)=$
设 $f(x)$ 是连续函数,且 $\int_0^{x^3-1} f(t) \mathrm{d} t=x$ ,则 $f(7)=$
$\lim _{x \rightarrow+0}\left(\frac{1}{\sqrt{x}}\right)^{\tan x}=$
$\int_0^4 e^{\sqrt{x}} \mathrm{~d} x=$
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $f(x)=e^{x^2}, f[\varphi(x)]=1-x$ ,且 $\varphi(x) \geq 0$ ,求 $\varphi(x)$ 并写出它的定义域.
已知 $y=1+x e^{x y}$, 求 $\left.y^{\prime}\right|_{x=0}$ 及 $\left.y^{\prime \prime}\right|_{x=0}$
求微分方程 $y^{\prime}+\frac{1}{x} y=\frac{1}{x\left(x^2+1\right)}$ 的通解.
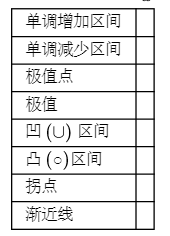
做函数 $ y=\frac{6}{x^2-2 x+4} $ 的图形,并填写下表
将长为 $a$ 的铁丝切成两段,一段围成正方形,另一段围成圆形,问这两段铁丝各长为多少时,正方形与圆形的面积之和为最小?
设函数 $y=y(x)$ 满足微分方程 $y^{\prime \prime}-3 y^{\prime}+2 y=2 e^x$ ,且其图形在点 $(0,1)$ 处的切线与曲线 $y=x^2-x+1$ 在该点的切线重合,求函数 $y=y(x)$.
设 $x \geq-1$ ,求 $\int_{-1}^x(1-|t|) \mathrm{d} t$.
设 $f(x)$ 在 $(-\infty, \infty)$ 上有连续导数,且 $m \leq f(x) \leq M$.
(1) 求 $A=\lim _{a \rightarrow+0} \frac{1}{4 a^2} \int_{-a}^a[f(t+a)-f(t-a)] \mathrm{d} t$ ;
(2)证明: $\left|\frac{1}{2 a} \int_{-a}^a f(t) \mathrm{d} t-f(x)\right| \leq M-m(a>0)$.