单选题 (共 7 题 ),每题只有一个选项正确
农户利用"立体大棚种植技术"把毛豆和芹菜进行混种,已知毛豆齐苗后棚湿在 $18 \sim 25^{\circ} \mathrm{C}$最适宜,播种芹菜的最适宜温度是 $15 \sim 20^{\circ} \mathrm{C}$ .农户在毛豆齐苗后在同一大棚播种了芹菜,这时应该把大棚温度设置在下列哪个范围最适宜( )
$\text{A.}$ $15 \sim 18^{\circ} \mathrm{C}$
$\text{B.}$ $18 \sim 20^{\circ} \mathrm{C}$
$\text{C.}$ $20 \sim 25^{\circ} \mathrm{C}$
$\text{D.}$ $20^{\circ} \mathrm{C}$ 以上
一元一次不等式组 $\left\{\begin{array}{l}x+7>1 \\ \frac{x-1}{3} \leqslant 4\end{array}\right.$ 解集为
$\text{A.}$  $\text{B.}$
$\text{B.}$ 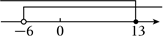 $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 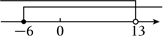
若关于 $x$ 的分式方程 $\frac{\mathrm{x}}{\mathrm{x}-3}-2=\frac{\mathrm{m}-1}{\mathrm{x}-3}$ 有增根,则 $m$ 的值为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
分式方程 $\frac{7}{x-8}=1$ 的解是
$\text{A.}$ $x=-1$
$\text{B.}$ $x=1$
$\text{C.}$ $x=15$
$\text{D.}$ $x=8$
"最是书香能致远,读书之乐乐无穷."为了传承和发扬中华民族优秀传统文化,丰富校园文化生活,提高全校师生的文化情操和艺术修养,让书香飘逸校园,某校推出"建设书香校园"的活动计划,购买了一批图书.已知购买科普类图书花费 30000 元,购买文学类图书花费 40000 元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵 10 元,且购买科普类图书的数量比购买文学类图书的数量少 1000 本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是 $x$ 元,则下列方程正确的是
$\text{A.}$ $\frac{30000}{x}-\frac{40000}{x-10}=1000$
$\text{B.}$ $\frac{40000}{x-10}-\frac{30000}{x}=1000$
$\text{C.}$ $\frac{30000}{x-10}-\frac{40000}{x}=1000$
$\text{D.}$ $\frac{40000}{x}-\frac{30000}{x-10}=1000$
已知关于 $x$ 的方程 $\frac{\mathrm{a}}{\mathrm{x}+1}=1$ 的解是负数,则 $a$ 的取值范围是
$\text{A.}$ $a < 1$
$\text{B.}$ $a \leqslant 1$
$\text{C.}$ $a < 1$ 且 $a \neq 0$
$\text{D.}$ $a \leqslant 1$ 或 $a \neq 0$
已知实数 $a, b, c$ 满足 $a+2 b=3 c$ ,则下列结论不正确的是( )
$\text{A.}$ $a-b=3(c-b)$
$\text{B.}$ $\frac{a-c}{2}=c-b$
$\text{C.}$ 若 $a>b$ ,则 $a>c>b$
$\text{D.}$ 若 $a>c$ ,则 $\mathrm{b}-\mathrm{a}>\frac{\mathrm{c}-\mathrm{a}}{2}$
填空题 (共 7 题 ),请把答案直接填写在答题纸上
方程 $\frac{5}{x}=\frac{7}{x+2}$ 的解为 $\qquad$
不等式组 $\left\{\begin{array}{l}2 x-1 \leqslant 1 \\ -2 x < 4\end{array}\right.$ 的整数解有 $\qquad$ 个.
在平面直角坐标系中,点 $P(m-1, m+2)$ 位于第一象限,则 $m$ 的取值范围为
若关于 $x$ 的一元一次不等式组 $\left\{\begin{array}{l}3 x+6>2(x+4) \\ x+1>a\end{array}\right.$ 的解集为 $x>2$ ,且关于 $y$ 的分式方程 $\frac{3-a y}{3-y}-\frac{3}{y-3}=1$ 的解是整数,则所有满足条件的整数 $a$ 的值之和是
已知关于 $x$ 的分式方程 $\frac{a}{2 x+3}-\frac{a-x}{x-5}=1$ 无解,则 $a$ 的值为
不等式 $2 x-6 \leqslant 5$ 的最大整数解是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式组:$\left\{\begin{array}{l}3(x+2)-x>4 \\ \frac{1+2 x}{3} \geqslant x-1\end{array}\right.$ .
某项电力工程按千米记工作量为 1150 千米.某工程队承担了此项工程的施工,在完成了 100 千米工作量后,该工程队改进施工技术和方案,每小时比原来多完成 20 千米工作量,结果共用了 50 小时完成了此项工程的施工任务.试问:该工程队改进施工技术和方案后每小时工作量是多少千米?
某超市用 1000 元购进一批商品,很快销售完毕,接着又用 1100 元购进第二批商品,已知两批商品的数量相等,且第一批商品每件的进货价比第二批商品每件进货价少 1 元.
(1)这两批商品进货价每件各是多少元?
(2)第一批商品以每件 16 元全部售出后,若想两批商品所得的利润率不低于 $50 \%$ ,则第二批商品每件的售价最少为多少元?
已知销售 1 部 $M$ 型手机和 1 部 $N$ 型手机共获利 500 元,销售 2 部 $M$ 型手机和 3 部 $N$ 型手机共获利 1200 元.
(1)请问 1 部 $M$ 型手机和 1 部 $N$ 型手机的利润分别为多少元?
(2)若某营业厅计划购进 $M, N$ 两种型号手机共 30 部,总利润不超过 7000 元,问 $N$ 型手机至少销售多少部?
经过我市全体市民的不懈努力, 2020 年娄底市获评"全国文明城市".为了巩固创文管卫的成果,我市园林部门准备在某路段种植香樟树(娄底市市树)和玉兰树两种树苗.已知购买 10 棵香樟树和 20 棵玉兰树共需 1100 元;购买 20 棵香樟树和 10 棵玉兰树共需 1000元。
(1)求购买 1 棵香樟树和 1 棵玉兰树各需多少元?
(2)若要购买这两种树苗共 600 棵,购买经费不超过 2 万元,问香樟树最少要购买多少棵?
八年(1)班学生周末乘汽车到抗美援朝纪念馆参观,纪念馆距离学校 60 km 。 一部分学生乘慢车先行,出发 $0.5 h$ 后,另一部分学生乘快车前往,结果他们同时到达纪念馆.已知快车的速度是慢车速度的 1.5 倍,求慢车的速度.