单选题 (共 4 题 ),每题只有一个选项正确
.如图所示,弹簧振子在A、B之间做简谐运动,O为平衡位置,测得A、B间距为6 cm,小球完成30次全振动所用时间为60 s,则
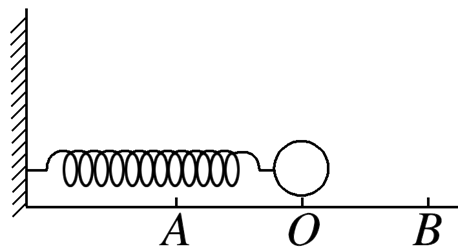
$\text{A.}$ 该振子振动周期是2 s,振幅是6 cm
$\text{B.}$ 该振子振动频率是2 Hz
$\text{C.}$ 小球完成一次全振动通过的路程是12 cm
$\text{D.}$ 小球过O点时开始计时,3 s内通过的路程为24 cm
扬声器是语音和音乐的播放装置,在生活中无处不在.如图所示是扬声器纸盆中心做简谐运动的振动图像,下列判断正确的是
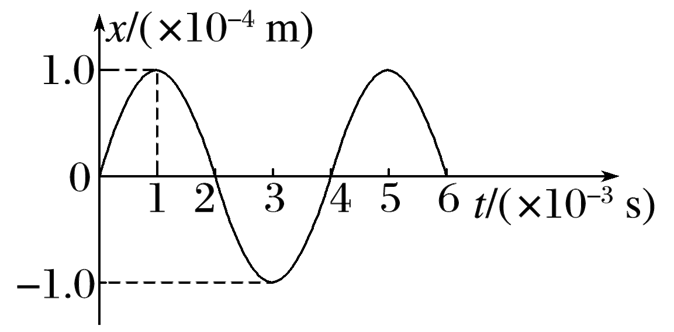
$\text{A.}$ $t=1 \times 10^{-3} s$ 时刻纸盆中心的位移最大
$\text{B.}$ $t=2 \times 10^{-3} s$ 时刻纸盆中心的加速度最大
$\text{C.}$ 在 $0 \sim 2 \times 10^{-3} s$ 之间纸盆中心的速度方向不变
$\text{D.}$ 纸盆中心做简谐运动的方程为 $x=1.0 \times 10^{-4} \cos 50 \pi t(m)$
如图所示,质量为m的物块放置在质量为M的木板上,木板与弹簧相连,它们一起在光滑水平面上做简谐运动,周期为T,振动过程中m、M之间无相对运动,设弹簧的劲度系数为k,物块和木板之间的动摩擦因数为μ,则下列说法正确的是

$\text{A.}$ 若 $t$ 时刻和 $(t+\Delta t)$ 时刻物块受到的摩擦力大小相等,方向相反,则 $\Delta t$ 一定等于 $\frac{T}{2}$ 的整数倍
$\text{B.}$ 若 $\Delta t=\frac{T}{2}$ ,则在 $t$ 时刻和 $(t+\Delta t)$ 时刻弹簧的长度一定相同
$\text{C.}$ 研究木板的运动,弹簧弹力充当了木板做简谐运动的回复力
$\text{D.}$ 当整体离开平衡位置的位移为 $x$ 时,物块与木板间的摩擦力大小等于 $\frac{m}{m+M} k x$
如图所示,两个摆长均为L的单摆,摆球A、B质量分别为m1、m2,悬点均为O.在O点正下方0.19L处固定一小钉.初始时刻B静止于最低点,其摆线紧贴小钉右侧,从图示位置由静止释放A(θ足够小),在最低点与B发生弹性正碰.两摆在整个运动过程中均满足简谐运动条件,摆线始终保持绷紧状态且长度不变,摆球可视为质点,不计碰撞
时间及空气阻力,重力加速度为g.下列选项正确的是

$\text{A.}$ 若 $m_1=m_2$ ,则 $A 、 B$ 在摆动过程中最大振幅之比为 $9: 10$
$\text{B.}$ 若 $m_1=m_2$ ,则每经过 $1.9 \pi \sqrt{\frac{L}{g}}$ 时间 $A$ 回到最高点
$\text{C.}$ 若 $m_1>m_2$ ,则 $A$ 与 $B$ 第二次碰撞不在最低点
$\text{D.}$ 若 $m_1 < m_2$ ,则 $A$ 与 $B$ 第二次碰撞必在最低点
多选题 (共 7 题 ),每题有多个选项正确
一水平弹簧振子做简谐运动的振动图像如图所示,已知弹簧的劲度系数为20 N/cm,则
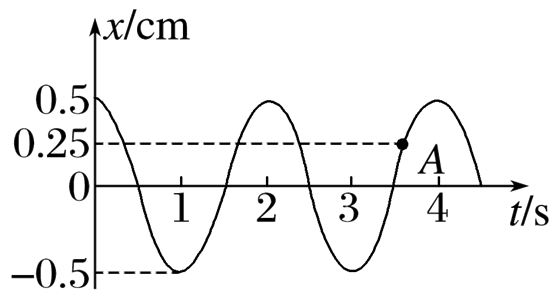
$\text{A.}$ 图中A点对应时刻振动物体所受的回复力大小为5 N,方向指向x轴的负方向
$\text{B.}$ 图中A点对应时刻振动物体的速度方向指向x轴的正方向
$\text{C.}$ 该振子的振幅等于0.5 cm
$\text{D.}$ 在0~4 s内振动物体做了1.75次全振动
如图所示,单摆在竖直平面内的A、C之间做简谐运动,O点为单摆的固定悬点,B点为运动中的最低位置,则下列说法正确的是

$\text{A.}$ 摆球在A点和C点时,速度为零,故细线拉力为零,但回复力不为零
$\text{B.}$ 摆球由A点向B点摆动过程中,细线拉力增大,但回复力减小
$\text{C.}$ 摆球在B点时,重力势能最小,机械能最小
$\text{D.}$ 摆球在B点时,动能最大,细线拉力也最大
很多高层建筑都会安装减震耗能阻尼器,用来控制强风或地震导致的振动.台北101大楼使用的阻尼器是重达660吨的调谐质量阻尼器,阻尼器相当于一个巨型质量块.简单说就是将阻尼器悬挂在大楼上方,它的摆动会产生一个反作用力,在建筑物摇晃时往反方向摆动,会使大楼摆动的幅度减小.关于调谐质量阻尼器下列说法正确的是

$\text{A.}$ 阻尼器做受迫振动,振动频率与大楼的振动频率相同
$\text{B.}$ 阻尼器与大楼摆动幅度相同
$\text{C.}$ 阻尼器摆动后,摆动方向始终与大楼的振动方向相反
$\text{D.}$ 阻尼器摆动幅度不受风力大小影响
甲、乙两弹簧振子的振动图像如图所示,则可知
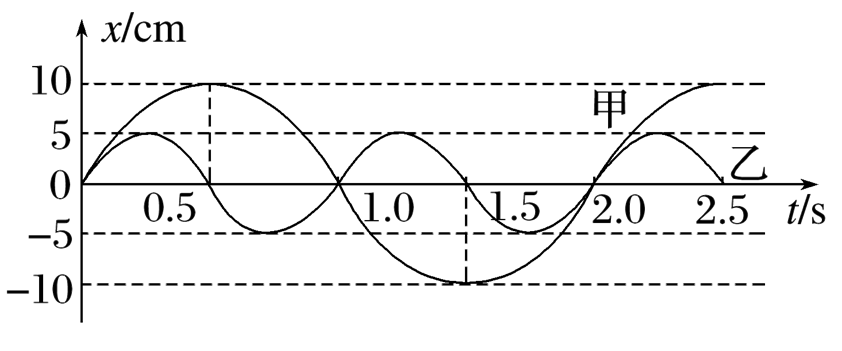
$\text{A.}$ 两弹簧振子完全相同
$\text{B.}$ 两弹簧振子所受回复力最大值之比F甲∶F乙=2∶1
$\text{C.}$ 振子甲速度为零时,振子乙速度最大
$\text{D.}$ 两振子的振动频率之比f甲∶f乙=1∶2
如图所示,表面光滑、半径为R的圆弧形轨道AP与水平地面平滑连接,AP弧长为s,s≪R.半径为r的小球从A点由静止释放,运动到最低点P时速度大小为v,重力加速度为g,则小球从A运动到P的时间是
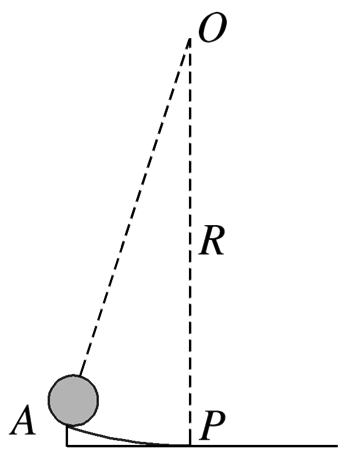
$\text{A.}$ $t=\frac{2 s}{v}$
$\text{B.}$ $t=\frac{\pi}{2} \sqrt{\frac{R-r}{g}}$
$\text{C.}$ $t=\frac{\pi}{4} \sqrt{\frac{R}{g}}$
$\text{D.}$ $t=\frac{\pi}{4} \sqrt{\frac{R-r}{g}}$
如图所示,倾角为θ、光滑的斜面体固定在水平面上,底端有垂直斜面的挡板,劲度系数为k的轻质弹簧下端拴接着质量为M的物体B,上端放着质量为m的物体P(P与弹簧不拴接).现沿斜面向下压一段距离后由静止释放,P就沿斜面做简谐运动,振动过程中,P始终没有离开弹簧.重力加速度为g,则
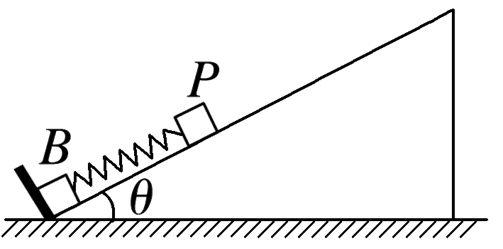
$\text{A.}$ $P$ 振动的振幅的最大值为 $\frac{m g \sin \theta}{k}$
$\text{B.}$ $P$ 振动的振幅的最大值为 $\frac{2 m g \sin \theta}{k}$
$\text{C.}$ $P$ 以最大振幅振动时,$B$ 对挡板的最大压力为 $M g \sin \theta+m g \sin \theta$
$\text{D.}$ $P$ 以最大振幅振动时,$B$ 对挡板的最大压力为 $M g \sin \theta+2 m g \sin \theta$
一振子沿x轴做简谐运动,平衡位置在坐标原点.t=0时振子的位移为-0.1 m,t=1 s时位移为0.1 m,则
$\text{A.}$ 若振幅为 0.1 m ,振子的周期可能为 $\frac{2}{3} s$
$\text{B.}$ 若振幅为 0.1 m ,振子的周期可能为 $\frac{4}{5} s$
$\text{C.}$ 若振幅为 0.2 m ,振子的周期可能为 4 s
$\text{D.}$ 若振幅为 0.2 m ,振子的周期可能为 6 s