解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知二次函数 $y=x^2+(m-2) x+\frac{1}{4}(m-4)(m-2)$ ,其中 $m>2$ .
(1)当该函数的图象经过原点 $O(0,0)$ ,求此时函数图象的顶点 $A$ 的坐标;
(2)求证:二次函数 $y=x^2+(m-2) x+\frac{1}{4}(m-4)(m-2)$ 的顶点在第三象限;
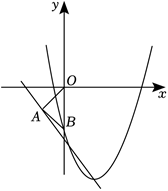
(3)如图,在(1)的条件下,若平移该二次函数的图象,使其顶点在直线 $y=-2 x-4$上运动,平移后所得函数的图象与 $y$ 轴的负半轴的交点为 $B$ ,求 $\triangle A O B$ 面积的最大值.
已知矩阵 $\boldsymbol{A}=\left(\begin{array}{ll}3 & 2 \\ 2 & 3\end{array}\right),(1)$ 求矩阵 $\boldsymbol{A}$ 的特征值和特征向量;(2)计算 $f(\boldsymbol{A})=\boldsymbol{A}^{n+1}-5 \boldsymbol{A}^*$ 。
证明题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $A, B$ 为 $n$ 阶方阵,$I$ 为 $n$ 阶单位矩阵,计算
$$
\left(\begin{array}{cc}
I & I \\
O & I
\end{array}\right)\left(\begin{array}{cc}
A & B \\
B & A
\end{array}\right)\left(\begin{array}{cc}
I & -I \\
O & I
\end{array}\right)
$$
并由此证明 $\left|\begin{array}{ll}A & B \\ B & A\end{array}\right|=|A+B| \cdot|A-B|$
设 $n$ 维向量 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 正交,证明 $\|\boldsymbol{a}+\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2$ .