单选题 (共 6 题 ),每题只有一个选项正确
设函数 $f(x)=|x|$, 则函数在点 $x=0$ 处
$\text{A.}$ 连续且可导
$\text{B.}$ 连续且可微
$\text{C.}$ 连续不可导
$\text{D.}$ 不连续不可微
$x=0$ 是函数 $f(x)=\arctan \frac{1}{x}$ 的
$\text{A.}$ 可去间断点
$\text{B.}$ 跳跃间断点
$\text{C.}$ 连续点
$\text{D.}$ 无穷间断点
函数 $f(x)$ 的定义域为 $(a, b)$, 导函数 $f^{\prime}(x)$ 在 $(a, b)$ 内的图像如图所示, 则函数 $f(x)$ 在 $(a, b)$ 内有极小值点
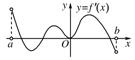
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
若 $\int f(x) d x=F(x)+C$, 则 $\int f(2 x+3) d x=$
$\text{A.}$ $F(2 x+3)$
$\text{B.}$ $2 F(2 x+3)+\mathrm{C}$
$\text{C.}$ $\frac{1}{2} F(2 x+3)$
$\text{D.}$ $\frac{1}{2} F(2 x+3)+C$
函数 $f(x)$ 在 $[a, b]$ 上连续是 $f(x)$ 在 $[a, b]$ 上可积的
$\text{A.}$ 充要条件
$\text{B.}$ 必要条件
$\text{C.}$ 充分条件
$\text{D.}$ 非必要非充分条件
下列反常积分发散的是
$\text{A.}$ $\int_1^{+\infty} \frac{1}{x^2} d x$
$\text{B.}$ $\int_0^1 \frac{x d x}{\sqrt{1-x^2}}$
$\text{C.}$ $\int_0^1 \frac{1}{\sqrt{x}} d x$
$\text{D.}$ $\int_1^{+\infty} \frac{1}{x \ln x} d x$