如图是由边长为1的若干正方形拼成的图像，其中第一个图像有1个正方形组成，周长为4，第二个图像由4个正方形组成，变成为10，第3个图像由9个正方形组成，变成为16.。。
(1) 第4 个图形由 个正方形组成。周长为
(2) 第n 个图形由 个正方形组成。周长为
(3) 若某个图像的周长为58，该图形由多少个正方形拼成？

如图①, 在长方形 $A B C D$ 中, $A B=12 \mathrm{~cm}, B C=6 \mathrm{~cm}$. 点 $P$ 沿 $A B$ 边从点 $A$ 开始向点 $B$ 以 $2 \mathrm{~cm} / \mathrm{s}$ 的速度移动,点 $Q$ 沿 $D A$ 边从点 $D$ 开始向点 $A$ 以 $1 \mathrm{~cm} / \mathrm{s}$ 的速度移动.


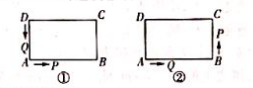
设点 $P, Q$ 同时出发,用 $t(\mathrm{~s})$ 表示移动的时间.
【发现】 $D Q=$ $\mathrm{cm}, A P=$ $\mathrm{cm}$. (用含 $t$ 的代数式表示)

【拓展】 (1) 如图①, 当 $t=$ $\mathrm{s}$ 时,线段 $A Q$ 与线段 $A P$ 相等;
(2) 如图②, 点 $P, Q$ 分别到达点 $B, A$ 后继续运动, 点 $P$ 到达点 $C$ 后停止运动. 当 $t$ 为何值时, $A Q=\frac{1}{2} C P$ ?

【探究】若点 $P, Q$ 分别到达点 $B, A$ 后继续沿着 $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ 的方向运动, 请直接写出点 $P$ 与点 $Q$ 第一次相遇时, 相遇点的位置.

设 $f(x)$ 有二阶连续导数, 在 $x=0$ 的去心邻域内 $f(x) \neq 0, \lim _{x \rightarrow 0} \frac{f(x)}{x}=0, \lim _{x \rightarrow 0}\left[1+x+\frac{f(x)}{x}\right]^{\frac{1}{x}}=e^3$,求 $f^{\prime \prime}(0)$ 及 $\lim _{x \rightarrow 0}\left[1+\frac{f(x)}{x}\right]^{\frac{1}{x}}$