单选题 (共 6 题 ),每题只有一个选项正确
设 $X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的简单随机样本, 其中 $P(X=0)=P(X=1)=\frac{1}{2}, \Phi(x)$ 表 示标准正态分布函数, 则利用中心极限定理可得 $P\left(\sum_{i=1}^{100} X_i \leq 55\right)$ 的近似值为
$\text{A.}$ $1-\Phi(1)$
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $1-\Phi(2)$
$\text{D.}$ $\Phi(2)$
设随机变量 $X, Y$ 相互独立, 且 $X \sim E(a), Y \sim E(b)(a>0, b>0, a \neq b)$, 则服从 $E(a+b)$ 的 随机变量是
$\text{A.}$ $X+Y$.
$\text{B.}$ $X Y$.
$\text{C.}$ $\max \{X, Y\}$.
$\text{D.}$ $\min \{X, Y\}$.
设 $X_1, X_2, \cdots, X_8$ 为来自总体 $X \sim N\left(0, \sigma^2\right)$ 的简单随机样本, $Y^2=\frac{1}{8} \sum_{i=1}^8 X_i^2$, 则 下列选项正确的是
$\text{A.}$ $X^2 \sim \chi^2(1)$.
$\text{B.}$ $Y^2 \sim \chi^2(8)$
$\text{C.}$ $\frac{X}{Y} \sim t(8)$.
$\text{D.}$ $\frac{X^2}{Y^2} \sim F(8,1)$.
三个随机事件 $A, B, C$ 相互独立的充分条件是
$\text{A.}$ $A, B, C$ 两两独立.
$\text{B.}$ $P(A+B+C)=1-P(\bar{A}) P(\bar{B}) P(\bar{C})$.
$\text{C.}$ $P(A B C)=P(A) P(B) P(C)$.
$\text{D.}$ $P(B-A)=1$.
设随机变量 $X$ 与 $Y$ 相互独立, 且 $X \sim N(0,1)$,
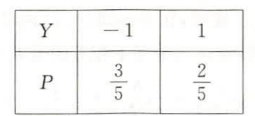
令随机变量 $Z=X Y$, 则 $Z$ 的分布为
$\text{A.}$ $N(-1,1)$.
$\text{B.}$ 与 $Y$ 同分布.
$\text{C.}$ $N(0,1)$.
$\text{D.}$ $N\left(\frac{1}{3}, \frac{2}{3}\right)$.
设 $F_1(x)$ 与 $F_2(x)$ 分别为随机变量 $X_1$ 与 $X_2$ 的分布函数, 为了使 $F(x)=a F_1(x)-b F_2(x)$ 是某一随机变量的分布函数, 则下列个组中应取
$\text{A.}$ $a=-\frac{1}{2}, b=\frac{3}{2}$
$\text{B.}$ $a=\frac{2}{3}, b=\frac{2}{3}$
$\text{C.}$ $a=\frac{3}{5}, b=-\frac{2}{5}$
$\text{D.}$ $a=\frac{1}{2}, b=-\frac{3}{2}$