单选题 (共 11 题 ),每题只有一个选项正确
计算 $a^6 \div a^3$
$\text{A.}$ $a^2$
$\text{B.}$ $a^3$
$\text{C.}$ $a^{-3}$
$\text{D.}$ $a^9$
如果 $\mathrm{a} < \mathrm{b}$, 则下列各式中成立的是
$\text{A.}$ $a+4>b+4$
$\text{B.}$ $a-b>b-6$
$\text{C.}$ $2+3 a>2+3 b$
$\text{D.}$ $-3 a>-3b$
已知 $\left\{\begin{array}{l}x=-2 \\ y=1\end{array}\right.$ 是方程 ${mx}+\mathrm{y}=3$ 的解, $\mathrm{m}$ 的值是
$\text{A.}$ 3
$\text{B.}$ -2
$\text{C.}$ 1
$\text{D.}$ -1
2024 年 5 月 26 日, 中国一新加坡工业园区开发建设 15 周年, 在这 15 年间实际利用外资 16200000000 美元, 用科学记数法表示为
$\text{A.}$ $1.62 \times 10^8$ 美元
$\text{B.}$ $1.62 \times 10^{10}$ 美元
$\text{C.}$ $162 \times 10^8$ 美元
$\text{D.}$ $0.162 \times 10^{11}$美元
为了解我市中学生中 15 岁女生的身高状况, 随机抽商了 10 个学校的 200 名 15 岁女生的身高, 则下列表述正确的是
$\text{A.}$ 总体指我市全体 15 岁的女中学生
$\text{B.}$ 个体是 10 个学校的女生
$\text{C.}$ 个体是 200 名女生的身高
$\text{D.}$ 抽查的 200 名女生的身高是总体的一个样本
有一个两位数, 它的十位数数字与个位数字之和为 5 , 则符合条件的数有
$\text{A.}$ 4 个
$\text{B.}$ 5 个
$\text{C.}$ 6 个
$\text{D.}$ 无数个
下列说法正确的是
$\text{A.}$ 调查某灯泡厂生产的 10000 只灯泡的使用寿命不宜用普查的方式.
$\text{B.}$ 2012 年奥运会刘翔能夺得男子 110 米栏的冠军是必然事件.
$\text{C.}$ 为了了解我市今夏冰淇淋的质量, 应采用普查的调查方式进行.
$\text{D.}$ 某种彩票中奖的概率是 $1 \%$, 买 100 .张该种彩票一定会中奖.
下列条件中, 不能判定 $\triangle A B C \cong \triangle A^{\prime} B^{\prime} C^{\prime}$ 的是
$\text{A.}$ $\angle \mathrm{A}=\angle \mathrm{A}, \angle \mathrm{C}=\angle \mathrm{C}, \mathrm{AC}=\mathrm{A}^{\prime} \mathrm{C}^{\prime}$
$\text{B.}$ $\angle \mathrm{C}=\angle \mathrm{C}^{\prime}=90^{\circ}, \mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
$\text{C.}$ $\angle \mathrm{A}=\angle \mathrm{A}^{\prime}=80^{\circ}, \angle \mathrm{B}=60^{\circ}, \angle \mathrm{C}^{\prime}=40^{\circ}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
$\text{D.}$ $\angle \mathrm{A}=\angle \mathrm{A}, \mathrm{BC}=\mathrm{B}^{\prime} \mathrm{C}^{\prime}, \mathrm{AB}=\mathrm{A}^{\prime} \mathrm{B}^{\prime}$
现有纸片: 1 张边长为 $\mathrm{a}$ 的正方形, 2 张边长为 $\mathrm{b}$ 的正方形, 3 张宽为 $\mathrm{a}$ 、长为 $\mathrm{b}$ 的长方形, 用这 6 张纸片重新拼出一个长方形, 那么该长方形的长为:
$\text{A.}$ $a+b$
$\text{B.}$ $a-+2 b$
$\text{C.}$ $2 \mathrm{a}+\mathrm{b}$
$\text{D.}$ 无法确定
设 $a b c \neq 0$, 且 $a+b+c=0$, 则 $\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}+\frac{a b c}{|a b c|}$ 的值可能是
$\text{A.}$ 0
$\text{B.}$ $\pm 1$
$\text{C.}$ $\pm 2$
$\text{D.}$ 0 或土2
填空题 (共 3 题 ),请把答案直接填写在答题纸上
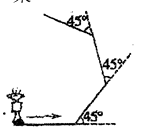
某科技小组制作了一个机器人, 它能根据指令要求进行行走和旋转. 某一指令规定: 机器人先向前行走 1 米, 然后互转 $45^{\circ}$, 若机器人反复执行这一指令, 则从出发到第一次回到原处, 机器人共走了 米.
下列各式是个位数位 5 的整数的平方运算:
$$
15^2 225 ; 25^2=625 ; 35^2=1225 ; 45^2=2025 ; 55^2=3025 ; 65^2=4225 ; \cdots \cdots \cdots ; 9995^2=\cdots
$$
观察这些数都有规律, 试利用该规律直接写出 $9995^2$ 运算的结果为
式子 $|x-1|+|x-2|+|x-3|+|x-4|+|x-5|+|x-6|+|x-7|+|x-8|+|x-9|+|x-10|$ 的最小值是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求值: $(x-y)^2+(x+y)(x-y)$, 其中 $x=3, y=-1$.
计算 $\left(\frac{1}{10}\right)^{-2}-(-3)^0+(-0.2)^{2009} \times(-5)^{2009}$
解不等式: $\frac{x+4}{2} \geq-\frac{2 x+1}{3}$, 并把它的解集在数轴上表示出来.
解方程组: $\left\{\begin{array}{l}\frac{x}{3}-\frac{y}{2}=1 \\ 3 x+2 y=-4\end{array}\right.$
按照指定要求画图
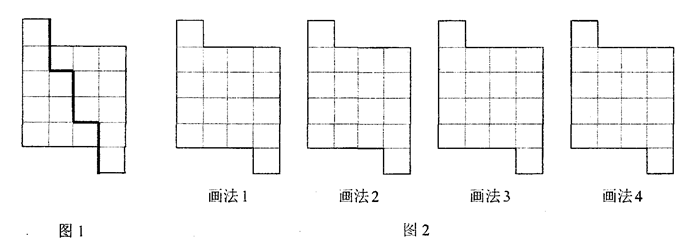
(1)如下图1所示,黑粗线把一个由18个小正方形组成的图形分割成两个全等图形,
请在图2中,仿图1沿着虚线用四种不同的画法,把每图形分割成两个全等图形.
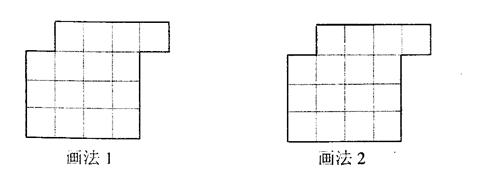
(2)请将下面由16个小正方形组成的图形,用两种不同的画法沿正方形的网格线用粗线把它分割成两个全等图形
关于 $\mathrm{x}$ 的方程 $x-2 m=-3 x+4$ 与 $2-m=x$ 的解互为相反数.
(1) 求 $m$ 的值;
(2) 求这两个方程的解.