2024年上海市初中毕业统一学业考试数学试卷(部分)

导出试卷

2024年上海市初中毕业统一学业考试数学试卷(部分)

一、单选题（共 2 题），每题只有一个选项正确

1. 四边形

A B C D

为矩形, 过

A 、 C

作对角线

B D

的垂线, 过

B 、 D

作对角线

A C

的垂线. 如果四个垂线拼成一个四边形,那这个四边形为

A.

菱形

B.

矩形

C.

直角梯形

D.

等腰梯形

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 在

△ A B C

中,

A C = 3, B C = 4, A B = 5

, 点

P

在

A B C

内, 分别以

A B P

为圆心画圆, 圆

A

半径为 1 , 圆

B

半径为 2 , 圆

P

半径为 3 , 圆

A

与圆

P

内切, 圆

P

与圆

B

的关系是

A.

内含

B.

相交

C.

外切

D.

相离

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 3 题），请把答案直接填写在答题纸上

3. 一个袋子中有若干个白球和绿球, 它们除了颜色外都相同. 随机从中摸一个球, 恰好摸到绿球的概率是

\frac{3}{5}

, 则袋子中至少有

个绿球.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 在平行四边形

A B C D

中,

∠ A B C

是锐角, 将

C D

沿直线 1 翻折至

A B

所在直线, 对应点分别为

C^{'}, D^{'}

, 若

A C^{'} : A B : B

C = 1 : 3 : 7

, 则

\cos ∠ A B C =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 对于一个二次函数

y = a (x - m)^{2} + k (a \neq 0)

中存在一点

P (x^{'}, y^{'})

, 使得

x^{'} - m = y^{'} - k \neq 0

, 则称

2 | x^{'} - m |

为该抛物线的 “开口大小”, 那么抛物线

y = - \frac{1}{2} x^{2} + \frac{1}{3} x + 3

“开口大小”为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 4 题），解答过程应写出必要的文字说明、证明过程或演算步骤

6. 在平面直角坐标系

x O y

中, 反比例函数

y = \frac{k}{x} (k

为常数且

k \neq 0)

上有一点

A (- 3, m)

, 且与直线

y =

- 2 x + 4

交于另一点

B (n, 6)

.
(1) 求

k

与

m

的值；
(2) 过点

A

作直线

l ∥ x

轴与直线

y = - 2 x + 4

交于点

C

, 求

\sin ∠ O C A

的值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

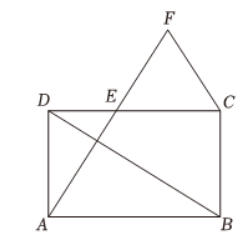
7. 如图所示, 在矩形

A B C D

中,

E

为边

C D

上一点, 且

A E ⊥ B D

.
(1) 求证:

A D^{2} = D E \cdot D C

；
( 2 )

F

为线段

A E

延长线上一点, 且满足

E F = C F = \frac{1}{2} B D

, 求证:

C E = A D

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 在平面直角坐标系中, 已知平移抛物线

y = \frac{1}{3} x^{2}

后得到的新抛物线经过

A (0, - \frac{5}{3})

和

B (5, 0)

.
（1）求平移后新抛物线的表达式；
（2）直线

x = m (m > 0)

与新抛物线交于点

P

, 与原抛物线交于点

Q

；
① 如果

P Q

小于 3 , 求

m

的取值范围；
② 记点

P

在原抛物线上的对应点为

P^{'}

, 如果四边形

P^{'} B P Q

有一组对边平行, 求点

P

的坐标.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 在梯形

A B C D

中,

A D ∥ B C

, 点

E

在边

A B

上, 且

A E = \frac{1}{3} A B

.
(1) 如图1所示, 点

F

在边

C D

上, 且

D F = \frac{1}{3} C D

, 联结

E F

, 求证:

E F ∥ B C

；
( 2) 已知

A D = A E = 1

；
① 如图2所示, 联结

D E

, 如果

△ A D E

外接圆的圆心恰好落在

∠ B

的平分线上, 求

△ A D E

的外接圆的半径长；
② 如图3所示, 如果点

M

在边

B C

上, 联结

E M 、 D M 、 E C, D M

与

E C

交于

N

. 如果

∠ D M C = ∠ C E M, B C = 4

, 且

C D^{2} = D M \cdot D N

, 求边

C D

的长.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。