一、单选题 (共 12 题 ),每题只有一个选项正确
1. 设二次函数 的图象的顶点为 , 与 轴的交点为 . 当 为等边三角形时, 其边长为
.
.
.
.
2. 如图, 在矩形
中,
的平分线交
于点
, 则
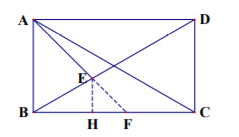
.
.
.
.
3. 设 均为大于 3 的素数, 则使 为完全平方数的素数对 的个数为
1
2
3
4
4. 若实数 满足 , 则
46 .
64 .
82 .
128.
5. 对任意的整数 , 定义 , 则使得 的整数组 的个数为
1
2
3
4
6. 设 , 则 的整数部分是
60
61
62
63
7. 满足 的整数 的个数为
1
2
3
4
8. 已知 为关于 的方程 的三个实数根, 则
5
6
7
8
9. 已知点
分别在正方形
的边
上,
, 则
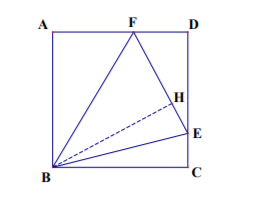
.
.
.
.
10. 方程 的实数根的个数为
0
1
2
3
11. 设 为三个实数, 它们中任何一个数加上其余两数之积的 2017 倍都等于 2018 , 则这样的三元数组 的个数为
4
5
6
7
12. 已知实数 满足 , 则
2
3
4
5
二、填空题 (共 8 题 ),请把答案直接填写在答题纸上
13. 如图, 在平行四边形
中,
于
为
的中点, 若
,则
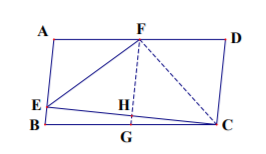
14. 若实数 满足 , 则 的最大值为
15. 没有重复数字且不为 5 的倍数的五位数的个数为
16. 已知实数 满足 , 则
17. 已知 为素数, 且 整除 , 则
18. 已知两个正整数的和比它们的积小 1000 , 若其中较大的数是完全平方数, 则较小的数为
19. 已知 是 内一点, 是 的中点, , , 则
20. 已知二次函数 的图象在 轴的上方, 则满足条件的正整数对 的个数为
三、解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
21. 设 为四个不同的实数, 若 为方程 的根, 为方程 的根, 求 的值.
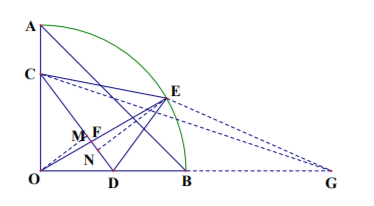
22. 如图, 在扇形
中,
, 点
在
上,
,点
为
的中点, 点
为弧
上的动点,
与
的交点为
.
(1) 当四边形
的面积
最大时, 求
;
(2) 求
的最小值.
23. 求所有的正整数 , 使得 是非负整数.
24. 若实数 满足 , 求 的值.
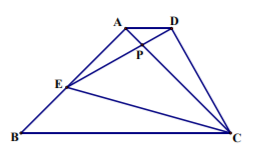
25. 如图, 点
在四边形
的边
上,
和
都是等腰直角三角形,
.
(1) 证明:
; (2) 设
与
交于点
, 如果
, 求
.
26. 设 是一个四位数, 的各位数字之和为 的各位数字之和为 , 并且 与 的最大公约数是一个大于 2 的素数. 求 .