一、单选题 (共 5 题 ),每题只有一个选项正确
1. 已知 , 则 的值是
22
23
24
25
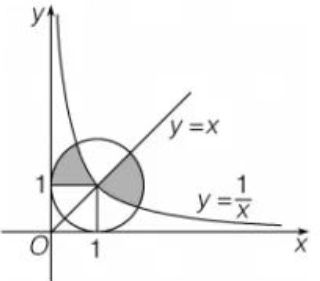
2. 在平面直角坐标系
中画有函数
和
的图象以及以点 ( 1 , 1) 为圆心半径为 1 的圆, 如图 1 所示. 则图中两块阴影部分的面积之和为
3. 如果关于 的方程 和 有公共实根, 则 等于
2
1
-2
-1
4. 在圆周上标出 720 个点, 恰分该圆周为 720 段相等的弧, 以这些分点为顶点的不同的正多边形的种数为
72
36
30
28
5. 已知三角形的三条边长 是互不相等的整数,且满足则此三角形的周长是
12
13
14
16
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
6. 设 为自然数, 与 都是某个不等于 1 的自然数 的倍数, 则
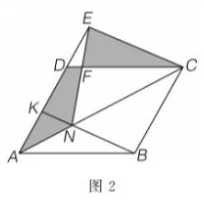
7. 如图 2 , 点
在平行四边形
的对角线
上, 点
在
的延长线上, 且
交
于点
的面积是 2019 , 则四边形
的面积
8. 对于如下四个判断: ① 被 5 整除; ② 被 23 整除; ③ 是完全平方数;④ 是完全平方数, 两位数 恰满足其中的两个. 所有这样的两位数之和等于
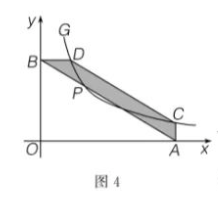
9. 如图 4, 点
是函数
的图象
上的一点, 过点
的直线分别交
轴、
轴于
、 两点. 过
作
轴的垂线, 交
于点
, 过
作
轴垂线, 交
于点
, 这时四边形
面积
10. 在 中, , 点 、 分别在 、 上, 且满足 , 、 分别为 、 的中点, 则 的度数等于
三、解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
11. 试确定 2019 能否表示为两个整数的立方和. 如果能, 请写出一种表示; 如果不能, 请说明理由.
12. 在凸四边形 中, , .
证明: .
13. 现有 10 个边长分别为 , 的正方形. 试问: 用这些正方形能否拼接(不许重叠, 不许中空) 成一个长方形? 如果能, 就给出这个长方形的长和宽, 并请画出拼接图.如果不能, 也请说明理由.