一、单选题 (共 4 题 ),每题只有一个选项正确
1. 已知集合 , 若 且, 则
2. 如图, 是某校随机抽取 50 名学生的身高与体重的 散点图, 则下列说法正确的是
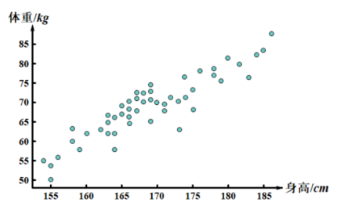
身高越高, 体重越重;
身高越高, 体重越轻;
身高与体重成正相关;
身高与体重成负相关.
3. 设 , 函数 在 上的最小值为 , 在 上的最小值为 , 当 变化时, 则下列选 项不可能的是
4. 在平面上, 若曲线 具有如下性质: 存在点 , 使得对于任意点 , 都有 使得 ,
则称这条曲线为 “自相关曲线” . 关于以下两个结论, 正确的判断是 ( )
(1) 所有椭圆都为 “自相关曲线” ; (2)存在双曲线是 “自相关曲线” .
(1)成立, (2)成立;
(1)成立, (2)不成立;
(1)不成立, (2)成立;
(1)不成立, (2)不成立.
二、填空题 (共 17 题 ),请把答案直接填写在答题纸上
6. 若 , 则
7. 已知 为等比数列 的前 项和, 且 , 则
9. 若函数 , 则 的值域为
10. 已知复数 (其中 为虚数单位), 则
11. 已知圆 的面积为 , 则
12. 在 中, 角 、、 所对的三边长分别为 、、, 若 , 则
13. 国内生产总值 (GDP) 是衡軍地区经济状况的最佳指标, 根据统计数据显示, 某市在 2020 年间经济高厉 量增长, 稳步增长, 第一季度和第四季度的 分别为 231 亿元和 242 亿元, 且四个季度 的 中位数与平均数相等, 则该市 2020 年 总额为 亿元.
14. 已知 , 其中 . 若 且 , 则当 时, 的最大值为
15. 某公园欲修建一段斜坡, 假设斜坡底端在水平地面上且坡面笔直, 斜坡顶端距水平地面的高度为 4 米, 斜 坡与水平地面的夹角为 . 已知游客从坡底沿着斜坡每向上走 1 米, 消耗的体力为 , 若要 使游客从斜坡底端走到斜坡顶端所消耗的体力最少, 则
16. 已知空间中存在三点 、、, 且 . 若从空间中再任取不同的两点 (不计顺序), 使得这两点与 、、 三点恰好能构成一个正四棱雉, 则不同的取法共有 种.
17. 如图, 在直四棱柱
中,
.
(1) 求证: 直线
平面
;
(2) 若直四棱柱
的体积为 36 , 求二面角
的大小.

18. 已知函数 , 其中 .
(1) 当 时, 求 的定义域, 并判断是否存在实数 , 使得 是奇函数;
(2) 若函数 的图像过点 , 且与 轴的负半轴有两个交点, 求实数 的值和实数 的取值范围.
19. 第二十届上海国际汽车工业展览会丁 2023 年 4 月 18 日在上海国家会展中心举行. 某汽车企业准备了 25 个汽车模型, 其外观和内饰的颜色分布如下表所示:

(1) 若小明从这些模型中随机拿一个模型, 记事件
为小明取到的横型为红色外观, 事件
为小明取到 的模型有米色内饰. 求
与
, 并据此判断事件
和事件
足否独立;
(2) 为了回馈客户, 该汽车企业举行了一个抽奖活动, 规定在一次抽奖中, 每人可以一次性抽取两个汽 车横型, 根据活动规则, 现作出如下假设:
该公司举行了一个扔奖活动, 并规定在一次排奖中, 每人可以一次性从这 25 个汽车模型中排取两 个, 现有如下假设:
假设 1: 抽取所得的两个模型会出现三种结果, 即外观和内饰均为同色、外观和内饰均为异色、只 有外观或只有内饰同色:
假设 2: 根据三种结果的可能性大小, 概率越小的结果可获得的奖项越高;
假设 3: 奖金额为一等奖 600 元, 二等奖 300 元, 三等奖 150 元.
请你帮该汽车企业分析假设 1 中的三种结果分别对应什么奖项, 设奖金额为
元, 与出
的分布列, 并 求出
的数学期望.
20. 已知抛物线 为第一象限内曲线 上的点, 设 的纵坐标是 .
(1) 若点 到抛物线 的准线距离为 3 , 求 的值;
(2) 若 , 点 在 轴上, 且 的中点在抛物线 上, 求点 的坐标和坐标原点 到直线 的 距离;
(3) 已知直线 是第一象限内曲线 上吕于点 的点, 直线 交 于点 , 且 在直线 上的投影为点 . 若对于任意点 恒成立, 求 的取值范围.
21. 已知函数 . 过点 作曲线 的切线交 轴于点 , 再过点 作曲线 的切线交 轴于 , 若 则停止. 以此类推, 得到数列 .
(1) 若正整数 , 证明: ;
(2) 若正整数 , 试比较 与 大小;
(3) 若正整数 , 是否存在 使得 依次成等差数列? 若存在, 求出 的所有取值; 若不 存在, 请说明理由.