单选题 (共 10 题 ),每题只有一个选项正确
一平面简谐波的表达式为 $y=0.1 \cos (3 \pi t-\pi x+\pi)(\mathrm{SI}), t=0$ 时的波形曲线如图所示,则
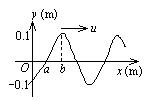
$\text{A.}$ $O$ 点的振幅为 $-0.1 \mathrm{~m}$
$\text{B.}$ 波长为 $3 \mathrm{~m}$
$\text{C.}$ $a 、 b$ 两点间相位差为 $\frac{1}{2} \pi$
$\text{D.}$ 波速为 $9 \mathrm{~m} / \mathrm{s}$
已知一平面简谐波的表达式为 $y=A \cos (a t-b x)(a 、 b$ 为正值常量 $)$ ,则
$\text{A.}$ 波的频率为 $a$
$\text{B.}$ 波的传播速度为 $b / a$
$\text{C.}$ 波长为 $\pi / b$
$\text{D.}$ 波的周期为 $2 \pi / a$
图为沿 $x$ 轴负方向传播的平面简谐波在 $t=0$ 时刻的波形. 若波的表达式以余弦函数表示, 则 $O$ 点处质点振动的初相为
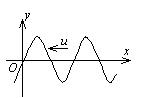
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{2} \pi$
$\text{C.}$ $\pi$
$\text{D.}$ $\frac{3}{2} \pi$
一横波沿 $x$ 轴负方向传播,若 $t$ 时刻波形曲线如图所示, 则在 $t+T / 4$ 时刻 $x$ 轴上的 $1 、 2 、 3$ 三点的振动位移分别是
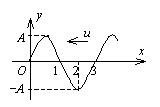
$\text{A.}$ $A, \quad 0,-4$
$\text{B.}$ $ A, \quad 0, \quad A$
$\text{C.}$ $0, \quad A, \quad 0$
$\text{D.}$ $0,-A, \quad 0$
如图所示, 有一平面简谐波沿 $x$ 轴负方向传播, 坐标原点 $O$ 的振动规律为 $\left.y=A \cos \left(\omega t+\phi_0\right)\right)$, 则 $B$ 点的振动方程为

$\text{A.}$ $y=A \cos \left[\omega t-(x / u)+\phi_0\right]$
$\text{B.}$ $y=A \cos \omega[t+(x / u)]$
$\text{C.}$ $y=A \cos \left\{\omega[t-(x / u)]+\phi_0\right\}$
$\text{D.}$ $y=A \cos \left\{\omega[t+(x / u)]+\phi_0\right\}$
一平面简谐波以速度 $u$ 沿 $x$ 轴正方向传播,在 $t=t^{\prime}$ 时波形曲线如图所示. 则坐标原点 $O$ 的振动方程为
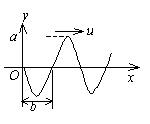
$\text{A.}$ $y=a \cos \left[\frac{u}{b}\left(t-t^{\prime}\right)+\frac{\pi}{2}\right]$
$\text{B.}$ $y=a \cos \left[2 \pi \frac{u}{b}\left(t-t^{\top}\right)-\frac{\pi}{2}\right]$
$\text{C.}$ $y=a \cos \left[\pi \frac{u}{b}\left(t+t^{\prime}\right)+\frac{\pi}{2}\right]$
$\text{D.}$ $y=a \cos \left[\pi \frac{u}{b}\left(t-t^{\prime}\right)-\frac{\pi}{2}\right]$
如图所示, 一平面简谐波沿 $x$ 轴正向传播, 已知 $P$ 点的振动方程为 $y=A \cos \left(\omega t+\phi_0\right)$, 则波的表达式为
$\text{A.}$ $y=A \cos \left\{\omega[t-(x-l) / u]+\phi_0\right\}$
$\text{B.}$ $y=A \cos \left\{\omega[t-(x / u)]+\phi_0\right\}$
$\text{C.}$ $y=A \cos \omega(t-x / u)$
$\text{D.}$ $y=A \cos \left\{\alpha[t+(x-l) / u]+\phi_0\right\}$
如图, 一平面简谐波以波速 $u$ 沿 $x$ 轴正方向传播, $O$ 为坐标原点. 已知 $P$ 点的振动方程为 $y=A \cos \omega t$, 则

$\text{A.}$ $O$ 点的振动方程为 $y=A \cos \omega(t-l / u)$
$\text{B.}$ 波的表达式为 $y=A \cos \omega[t-(l / u)-(l / u)]$
$\text{C.}$ 波的表达式为 $y=A \cos \omega[t+(l / u)-(x / u)]$
$\text{D.}$ C 点的振动方程为 $y=A \cos \omega(t-3 l / u)$
一平面简谐波沿x轴正方向传播,t= 0时刻的波形图如图所示,则P处质点的振动在t= 0时刻的旋转矢量图是

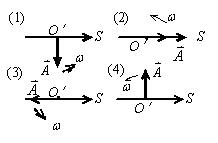
$\text{A.}$ (1)
$\text{B.}$ (2)
$\text{C.}$ (3)
$\text{D.}$ (4)
一平面简谐波沿 $O x$ 轴正方向传播, $t=0$ 时刻的波形图如图所示, 则 $P$ 处介质质点的振动方程是
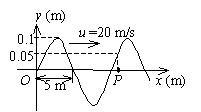
$\text{A.}$ $y_P=0.10 \cos \left(4 \pi t+\frac{1}{3} \pi\right)$(SI)
$\text{B.}$ $y_P=0.10 \cos \left(4 \pi t-\frac{1}{3} \pi\right)$(SI)
$\text{C.}$ $y_P=0.10 \cos \left(2 \pi t+\frac{1}{3} \pi\right)$ (SI)
$\text{D.}$ $y_P=0.10 \cos \left(2 \pi t+\frac{1}{6} \pi\right)$(SI)
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一平面简谐波沿 $x$ 轴正向传播, 其振幅为 $A$, 频率为 $v$, 波速为 $u$. 设 $t=t^{\prime}$ 时刻的波形曲线如图所示. 求
(1) $x=0$ 处质点振动方程;
(2) 该波的表达式 .
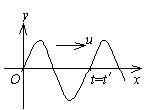
如图,一平面波在介质中以波速 $u=20 \mathrm{~m} / \mathrm{s}$ 沿 $x$ 轴负方向传播,已知 $A$ 点的振动方程为 $y=3 \times 10^{-2} \cos 4 \pi t$ (SI).
(1) 以 $A$ 点为坐标原点写出波的表达式;
(2) 以距 $A$ 点 $5 \mathrm{~m}$ 处的 $B$ 点为坐标原点, 写出波的表达式.
一平面简谐波沿 $x$ 轴正向传播,其振幅和角频率分别为 $A$ 和 $\omega$, 波速为 $u$, 设 $t=0$ 时的波形曲线如图所示.
(1)写出此波的表达式.
(2)求距 $O$ 点分别为 $\lambda / 8$ 和 $3 \lambda / 8$ 两处质点的振动方程.
(3)求距 $O$ 点分别为 $\lambda / 8$ 和 $3 \lambda / 8$ 两处质点在 $t=0$ 时的振动速度.

如图所示, 两相干波源在 $x$ 轴上的位置为 $S_1$ 和 $S_2$, 其间距离为 $d=30 \mathrm{~m}, S_1$ 位于坐标原点 $O$. 设波只沿 $x$ 轴正负方向传 播,单独传播时强度保持不变. $x_1=9 \mathrm{~m}$ 和 $x_2=12 \mathrm{~m}$ 处的两点是相邻的两个因干涉而静止的点. 求两波的波长和两波源间 最小相位差 .
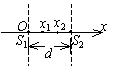
设入射波的表达式为 $y_1=A \cos 2 \pi\left(\frac{x}{\lambda}+\frac{t}{T}\right)$, 在 $x=0$ 处发生反射, 反射点为一固定端 . 设反射时无能量损失, 求
(1)反射波的表达式;
(2)合成的驻波的表达式;
(3)波腹和波节的位置.
在均匀介质中, 有两列余弦波沿 $O x$ 轴传播, 波动表达式分别为 $y_1=A \cos [2 \pi(\mathfrak{L}-x / \lambda)]{\text {与 }} y_2=2 A \cos [2 \pi(\mathcal{L}+x / \lambda)]$,
试求 $O x$ 轴上合振幅最 大与合振幅最小的那些点的位置.