2022年郑州外国语七年级（下）期末考试数学试卷及解析

导出试卷

2022年郑州外国语七年级（下）期末考试数学试卷及解析

一、单选题（共 10 题），每题只有一个选项正确

1. 下列各式中, 运算正确的是

A.

a^{3} + a^{2} = a^{5}

B.

(- a)^{2} \cdot (- a)^{3} = a^{5}

C.

{(a^{2})}^{3} = a^{5}

D.

a^{3} \cdot a^{2} = a^{5}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 据悉, 世界上最小的开花结果植物是澳大利亚的出水浮萍, 这种植物的果实像一个微小的无花果, 质量只有

0.00000009

克, 将数据

0.00000009

用科学记数法表示为

A.

9.0 \times 10^{- 8}

B.

9.0 \times 10^{- 9}

C.

9.0 \times 10^{8}

D.

0.9 \times 10^{9}

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

3. 下列图形中, 由

∠ 1 = ∠ 2

能得到

A B / / C D

的是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 下列多项式乘法中, 不能进行平方差计算的是

A.

(x + y) (- x - y)

B.

(2 a + b) (2 a - b)

C.

(- 3 x - y) (- y + 3 x)

D.

(a^{2} + b) (a^{2} - b)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 数学课上, 老师提出一个问题: 经过已知角一边上的点, 做一个角等于已知角. 如图, 用尺规过

A O B

的边

O B

上一点

C

(图①) 作

D C B A O B

(图②). 我们可以通过以下步骤
作图:

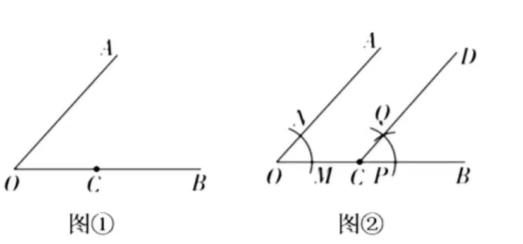
(1)作射线

C D

;
(2)以点

O

为圆心, 小于

O C

的长为半径作弧, 分别交

O A, O B

于点

N, M

,
(3)以点

P

为圆心,

M N

的长为半径作弧, 交上一段弧于点

Q

;
(4) 以点

C

为圆心,

O M

的长为半径作弧, 交

O B

于点

P

. 下列排序正碓的是

A.

(1)(2)(3)(4)

B.

(2)(4)(3)(1)

C.

(3)(2)(4) (1)

D.

(4)(3)(1)(2)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 2022 年 6 月 12 日, 京张高铁轨道全线贯通, 它是 2022 年北京冬奥会的重要交通保障设施. 全线运营后高铁将通过清华园隧道穿垡北京市城市核心区, 如图所示, 当高铁匀速通过清华园隧道 (隧道长大于火车长) 时, 高铁在隧道内的长度

y

与高铁进入隧道的时间

x

之间的关系用图象描述大致是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

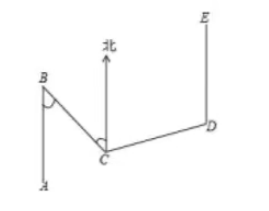
7. 如图, 小亮从

A

到达

E

, 路线为

A \to B \to C \to D \to E

. 由

A

到

B

和由

D

到

E

都是正北方向, 中间经历了 3 次拐弯, 第一次拐弯后, 行进方向变为南偏东

40^{\circ}

, 若

∠ D = 105^{\circ}

, 则

∠ B C D

的度数为

A.

100^{\circ}

B.

105^{\circ}

C.

110^{\circ}

D.

115^{\circ}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知

4 x^{2} - m x + 9

是完全平方式, 则

m

的值是

A.

6

B.

9

C.

\pm 9

D.

\pm 12

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 正方形的边长为 4 , 若边长增加

x

, 那么面积增加

y

, 则

y

关于

x

的函数表达式为

A.

y = x^{2} + 16

B.

y = (x + 4)^{2}

C.

y = x^{2} + 8 x

D.

y = 16 - 4 x^{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

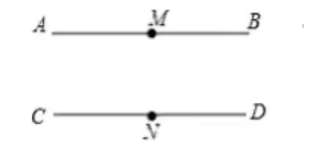
10. 现有甲、乙两个正方形纸片, 将甲、乙并列放置后得到图 1, 已知点

H

为

A E

的中点, 连结

D H, F H

. 将乙纸片放到甲的内部得到图 2. 已知甲、乙两个正方形边长之和为 6, 图 2 的阴影部分面积为 2 , 则图 1 的阴影部分面积为

A.

8

B.

9

C.

10

D.

11

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 5 题），请把答案直接填写在答题纸上

11. 已知

a^{m} = 4, a^{n} = 8

, 则

a^{m - n}

的值为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 已知一个角的补角是这个角的余角的 3 倍, 则这个角的度数是度.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 如图, 王老师把家里的 WIFI 密码设置成了数学问题. 吴同学来王老师家做客, 看到

W I F I

图片, 思索了一会儿, 输入密码, 顺利地连接到了王老师家里的网络, 那么她输入的密码是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

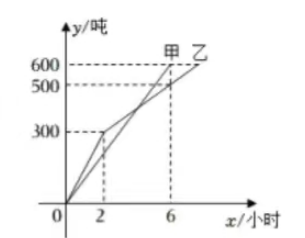
14. 14. 甲、乙两名码头工人同时从轮船上开始卸货, 他们每人都要卸下 600 旽货物, 他们所卸货物

y

(旽) 与卸货时间

x

(小时) 之间的关系如图所示, 则下列说法中正确的有 (填序号)
(1)甲每小时卸货 100 杶;
(2)前两个小时内, 乙每小时卸货 200 坉;
(3)乙需要 8 小时完成任务;
(4)当卸货时间为 2 小时或 6 小时时, 甲、乙两人所卸货物都相差 100 吨.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 如图, 直线

A B / / C D

, 点

M, N

分别在直线

A B, C D

上，点

E

为直线

A B

与

C D

之间的一点, 连接

M E, N E

, 且

∠ M E N = 110^{\circ}, ∠ A M E

的角平分线与

∠ C N E

的角平分线交于点

F

, 则

∠ M F N

的度数为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 6 题），解答过程应写出必要的文字说明、证明过程或演算步骤

16. (1)

16 \div (- 2)^{3} - {(\frac{1}{3})}^{- 1} + 20

;
(2) 先化简, 再求值

2 x (x - 3) - (x + 2) (x - 2)

, 其中

x = - 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

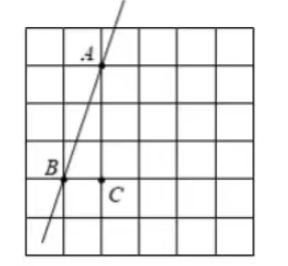
17. 如图所示的正方形网格, 点

A 、 B 、 C

都在格点上,
(1) 利用网格作图:
(1) 过点

C

画直线

A B

的平行线

C D

, 并标出平行线所经过的格点

D

;
(2)过点

C

画直线

A B

的垂线

C E

, 并标出垂线所经过的格点

E

, 垂足为点

F

;
(2) 线段的长度是点

C

到直线

A B

的距离;
(3) 比较大小:

C F

（　　）

C B

(填 > 、 < 或

=

), 理由是:

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 疫情期间, 全民检测, 人人有责. 某小区某时段进行核酸检测, 居民有序排队入场, 医务人员开始检测后, 现场排队等待检测人数

y

(人) 与时间

x

(分钟) 之间的关系式为

y

= 10 x + a

, 用表格表示为:

医务人员已检测的总人数 (人) 与时间 (分钟) 之间的关系如图所示:
(1) 图中表示的自变量是
(2) 图中点

A

表示的含义是
，因变量是
(3) 在医务人员开始检测 4 分钟时, 现堟阬等待检测的人数有人;
(4) 关系式

y = 10 x + a

中,

a

的值为
(5) 医务人员开始检测（　　）分钟后, 现场排队等待检测人数与医务人员已检测的总
人数相同;
(6) 如果该小区共有居民 1000 人, 那么医务人员全部检测完该小区居民共需（　　）分钟.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 阅读下文, 寻找规律:
已知:

x \neq 1

, 观察下列各式?

\begin{aligned} (x - 1) (x + 1) = x^{2} - 1; \\ (x - 1) (x^{2} + x + 1) = x^{3} - 1; \\ (x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1; \\ (x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1; \\ \dots \end{aligned}

(1) 填空:
①

(x - 1) (x^{9} + x^{8} + \dots + x^{2} + x + 1) =

②

(1 - x) (1 + x + x^{3} + \dots + x^{n - 1} + x^{n}) =

（2）根据你的猜想, 计算:
①

2^{2020} + 2^{2019} + 2^{2018} + \dots + 2 + 1 =

②那么

2^{2020} + 2^{2019} + 2^{2018} + \dots + 2 + 1

的末尼数字为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 【探究】
若

x

满足

(9 - x) (x - 4) = 4

, 求

(x - 4) 2 + (9 - x)^{2}

的值.
设

9 - x = a, x - 4 = b

, 则

(9 - x) (x - 4) = a b = 4, a + b = (9 - x) + (x - 4) = 5

∴ (9 - x)^{2} + (x - 4) 2 = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 5^{2} - 2 \times 4 = 17;

【应用】
请仿照上面的方法求解下面问题:
(1) 若

x

满足

(5 - x) (x - 2) = 2

, 求

(5 - x)^{2} + (x - 2)^{2}

的值;
【拓展】
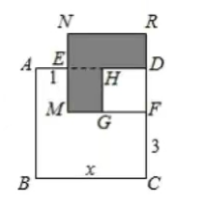
(2) 已知正方形

A B C D

的边长为

x, E, F

分别是

A D 、 D C

上的点, 且

A E = 1, C F = 3

, 长方形

E M F D

的面积是 8 , 分别以

M F 、 D F

为边作正方形.
(1)

M F =

，

D F =

（用含

x

的式子表示）
(2)求阴影部分的面积.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 在小学我们学过三角形的内角和等于

180^{\circ}

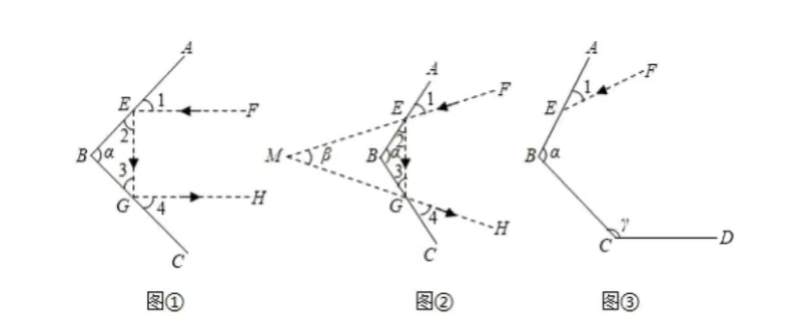
; 科学实验又证明, 平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等. 例如：在图(1)、图(2) 中, 都有

∠ 1 = ∠ 2, ∠ 3 = ∠ 4

. 设镜子

A B

与

B C

的夹角

∠ A B C = α

.
(1) 如图①, 若

α = 90^{\circ}, ∠ 1 = 50^{\circ}

, 则

∠ 4 =

(2) 如图②, 若

α = 115^{\circ}

, 入射光线

E F

与反射光线

G H

的夹角

∠ F M H = β

. 求

β

的度数;
(3) 如图③, 若

90^{\circ} < α < 180^{\circ}

, 设镜子

C D

与

B C

的夹角

∠ B C D = γ (90^{\circ} < γ < 180

)), 入射光线

E F

与镜面

A B

的夹角

∠ 1 = m (0^{\circ} < m < 90^{\circ})

, 已知入射光线

E F

从镜面

A B

反射到镜面

B C

, 再反射到镜面

C D

, 最后经镜面

C D

反射后, 当反射光线与入射光线

E F

平行时, 探索

m

与

γ

的数量关系, 并说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。