单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $A=\left\{x \in \mathbf{Z} \mid-\frac{6}{x} \in \mathbf{N}\right\}, B=\{x \mid x=2 t+3, t \in A\}$, 则 $A \cap B=$
$\text{A.}$ $\{-1,1,-3\}$
$\text{B.}$ $\{-1,-3\}$
$\text{C.}$ $\{-1,-3,-6\}$
$\text{D.}$ $\{-1,1,-3,-6\}$
已知 $\mathrm{i}$ 为虚数单位, $z=a+b \mathrm{i}(a, b \in \mathbf{R})$, 若 $(\bar{z}+1-a)[z+(1-b) \mathrm{i}]=-2 a \mathrm{i}$, 则复数 $z$ 在 复平面上对应的点位于
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
等额分付资本回收是指起初投资 $P$, 在利率 $i$, 回收周期数 $n$ 为定值的情况下, 每期期末 取出的资金 $A$ 为多少时, 才能在第 $n$ 期期末把全部本利取出, 即全部本利回收, 其计算 公式为: $A=P \cdot \frac{i(1+i)^n}{(1+i)^n-1}$. 某农业种植公司投资 33 万元购买一大型农机设备, 期望投 资收益年利率为 $10 \%$, 若每年年底回笼资金 $8.25$ 万元, 则该公司将至少在 ( ) 年内 能全部收回本利和. ( $\lg 11 \approx 1.04, \lg 5 \approx 0.70, \lg 3 \approx 0.48$ )
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
在 $\left(1-\frac{2}{x}\right)\left(1+\frac{1}{x}\right)^5$ 的展开式中, $\frac{1}{x^3}$ 的系数为
$\text{A.}$ $-30$
$\text{B.}$ $-20$
$\text{C.}$ $-10$
$\text{D.}$ $30$
执行如下图所示的程序框图, 则输出的 $T$ 为
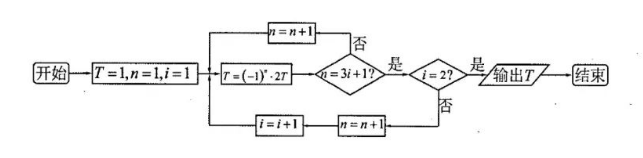
$\text{A.}$ $128$
$\text{B.}$ $-32$
$\text{C.}$ $16$
$\text{D.}$ $-64$
已知圆 $C: x^2+y^2+2 x-3=0$ 与过原点 $O$ 的直线 $l: y=k x(k \neq 0)$ 相交于 $A, B$ 两点, 点 $P(m, 0)$ 为 $x$ 轴上一点, 记直线 $P A, P B$ 的斜率分别为 $k_1, k_2$, 若 $k_1+k_2=0$, 则实数 $m$ 的 值为
$\text{A.}$ $-3$
$\text{B.}$ $-2$
$\text{C.}$ $2$
$\text{D.}$ $3$
如图, 在平行四边形 $A B C D$ 中, $\overrightarrow{A B}=2 \overrightarrow{A E}, \overrightarrow{A F}=\overrightarrow{F D}$, 点 $G$ 为 $C E$ 与 $B F$ 的交点, 则 $\overrightarrow{A G}=$
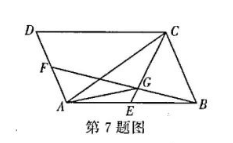
$\text{A.}$ $\frac{2}{5} \overrightarrow{A B}+\frac{1}{5} \overrightarrow{A C}$
$\text{B.}$ $\frac{1}{5} \overrightarrow{A B}+\frac{2}{5} \overrightarrow{A C}$
$\text{C.}$ $\frac{1}{5} \overrightarrow{A B}+\frac{4}{15} \overrightarrow{A C}$
$\text{D.}$ $\frac{3}{10} \overrightarrow{A B}+\frac{2}{5} \overrightarrow{A C}$
已知函数 $f(x)=2 \sin (\omega x+\varphi)\left(\omega \in \mathbf{N}^*, 0 < \varphi < \frac{\pi}{2}\right)$ 的部分图象如图所示, 且函数 $f(x)$ 在 $x=\frac{7 \pi}{12}$ 处取得最小值, 则函数 $f\left(\frac{x}{2}\right)$ 在 $[0, \pi]$ 上的单调递减区间为
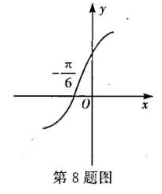
$\text{A.}$ $\left[0, \frac{\pi}{6}\right]$
$\text{B.}$ $\left[\frac{\pi}{6}, \frac{5 \pi}{6}\right]$
$\text{C.}$ $\left[0, \frac{\pi}{12}\right]$
$\text{D.}$ $\left[\frac{\pi}{6}, \pi\right]$
在四棱锥 $S-A B C D$ 中, $S C \perp$ 平面 $A B C D, A B / / C D, A B \perp A D, A D=C D=1, S D=$ $A B=2$, 点 $E$ 为 $S B$ 的中点, 则异面直线 $S D$ 与 $C E$ 所成角的余弦值为
$\text{A.}$ $\frac{\sqrt{5}}{10}$
$\text{B.}$ $\frac{\sqrt{5}}{5}$
$\text{C.}$ $\frac{2 \sqrt{5}}{5}$
$\text{D.}$ $\frac{3 \sqrt{5}}{10}$
如图, 已知长方体 $A B C D-A_1 B_1 C_1 D_1$ 的体积为 $16, A B=$ $2 A A_1=2 B C, A D_1$ 与 $A_1 D$ 相交于点 $E$, 则三棱锥 $E-A C D$ 的外接球的表面积为
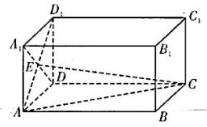
$\text{A.}$ $12 \pi$
$\text{B.}$ $16 \pi$
$\text{C.}$ $20 \pi$
$\text{D.}$ $36 \pi$
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1, F_2$, 点 $P$ 为第一象限内双 曲线上的点, 点 $Q$ 为点 $P$ 关于原点 $O$ 的对称点. 若 $|O P|=\left|O F_2\right|, 2\left|Q F_1\right| \leqslant\left|P F_1\right| \leqslant$ $3\left|Q F_1\right|$, 则双曲线 $C$ 的离心率的取值范围为
$\text{A.}$ $\left(1, \frac{\sqrt{10}}{2}\right]$
$\text{B.}$ $\left[\frac{\sqrt{10}}{2}, \sqrt{5}\right]$
$\text{C.}$ $(1, \sqrt{5}]$
$\text{D.}$ $[2, \sqrt{5}]$
已知 $f(x), g(x)$ 是定义在 $\mathbf{R}$ 上的函数, 且均不恒为零. $g(x)$ 为偶函数, $f(10)=-3$. 若 对任意的 $x \in \mathbf{R}$, 都有 $f(x+4)+f(x)=\sqrt{2} f(x+2)$, 设 $h(x)=(x-2) \cdot g(x)$, 若函数 $h(x+2)$ 的图象关于 $y$ 轴对称, 则下列说法正确的是
$\text{A.}$ 函数 $f(x)$ 的一个周期为 8
$\text{B.}$ 函数 $g(x)$ 的图象关于直线 $x=6$ 对称
$\text{C.}$ 函数 $g(x)$ 的一个周期为 4
$\text{D.}$ $f(98)+g(98)=3$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
小明的外婆来到蔬菜超市, 准备从黄瓜、南瓜、丝瓜、苦瓜、白瓜这 5 种新鲜瓜类蔬菜中 任意购买 3 种, 则小明的外婆购买的瓜类蔬菜中含苦瓜的概率为
已知点 $P\left(x_0, y_0\right)$ 关于 $x$ 轴的对称点在曲线 $C: y=2 \sqrt{2 x}$ 上, 且过点 $P$ 的直线 $y=x-2$ 与曲线 $C$ 相交于点 $Q$, 则 $|P Q|=$
已知数列 $\left\{a_n\right\}$ 的通项公式为 $a_n=\left(-\frac{4}{5}\right)^n \cdot \frac{n+1}{2}$, 设数列 $\left\{a_n\right\}$ 的最大项和最小项分别 为 $M, N$, 则 $M+N=$
已知直线 $y=k x+b$ 为曲线 $f(x)=\ln x$ 的一条切线, 则 $k \cdot b$ 的取值范围为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知各项均为正数的数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, a_1=1$, 且 $\frac{S_n}{S_{n+1}}=\frac{a_{n+1}-1}{a_{n+1}+1}$.
(1)求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=\frac{a_n}{3^{a_n-1}}$, 且数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $T_n$, 求证: $T_n < \frac{9}{4}$.
在斜三角形 $A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 满足 $a \sin A+4 b \sin C \cos ^2 A=$ $b \sin B+c \sin C$.
(1)求角 $A$ 的大小;
(2) 当 $a=3$ 时, 求 $b+c$ 的取值范围.
随着电池充电技术的逐渐成熟, 以锂电池为动力的新一代无绳类电动工具, 以其轻巧 便携、工作效率高、环保、可适应多种应用场景下的工作等优势, 被广泛使用. 在消费者便携无绳化需求与技术发展的双重驱动下, 锂电类无绳电动工具及配套充电器市场有望持续扩大. 某公司为适应市场并增强市场竞争力, 逐年增加研发人员, 使得整体研发 创新能力持续提升, 现对 2017 2021 年的研发人数作了相关统计, 如下图:
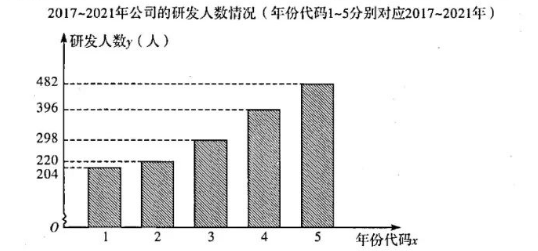
(1)根据条形统计图中数据, 计算该公司研发人数 $y$ 与年份代码 $x$ 的相关系数 $r$, 并由 此判断其相关性的强弱;
(2)试求出 $y$ 关于 $x$ 的线性回归方程,并预测 2023 年该公司的研发人数. (结果取整 娄)
参考数据 : $\sum_{i=1}^5\left(y_i-\bar{y}\right)^2=55960, \sqrt{1399} \approx 37.4$.
参考公式: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \cdot \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$.
线性回归方程的斜率 $\hat{b}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$, 截距 $\hat{a}=\bar{y}-\hat{b} \bar{x}$.
如图, 在直三棱柱 $A B C-A_1 B_1 C_1$ 中, $A B \perp B C$, 侧面 $A B B_1 A_1$ 为正方形, 点 $D, E, F, G$ 分别为棱 $A B, A C, B_1 C_1, A_1 B_1$ 的中点.
(1)求证: $G E / /$ 平面 $B C C_1 B_1$;
(2) 若二面角 $B_1-A_1 D-C$ 的余弦值为 $\frac{\sqrt{21}}{21}$, 且 $A B=2$, 求多面体 $A B C A_1 F C_1$ 的体积.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 上顶点为 $A$, 钝角三角形 $A F_1 F_2$ 的面积为 $\sqrt{3}$, 斜率为 $k$ 的直线 $l$ 交椭圆 $C$ 于 $P, Q$ 两点. 当直线 $l$ 经过 $F_1, A$ 两 点时, 点 $F_2$ 到直线 $l$ 的距离为 $\sqrt{3}$.
(1)求椭圆 $C$ 的标准方程;
(2) 设 $O$ 为坐标原点, 当直线 $l$ 的纵截距不为零时, 试问是否存在实数 $k$, 使得 $|\overrightarrow{P Q}|^2+$ $2 \overrightarrow{O P} \cdot \overrightarrow{O Q}$ 为定值? 若存在, 求出此时 $\triangle O P Q$ 面积的最大值; 若不存在, 请说明 理由.