2010 年全国统一高考数学试卷（理科）（新课标）

导出试卷

2010 年全国统一高考数学试卷（理科）（新课标）

一、单选题（共 12 题），每题只有一个选项正确

1. 已知集合

A = {x \in R | | x ∣⩽ 2}}, B = {x \in Z ∣ \sqrt{x} ⩽ 4}

, 则

A \cap B = (

)

A.

(0, 2)

B.

[0, 2]

C.

{0, 2}

D.

{0, 1, 2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 已知复数

z = \frac{\sqrt{3} + i}{(1 - \sqrt{3} i)^{2}}, \bar{z}

是

z

的共轭复数, 则

z = \bar{z} = ()

A.

\frac{1}{4}

B.

\frac{1}{2}

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 曲线

y = \frac{x}{x + 2}

在点

(- 1, - 1

) 处的切线方程为（）

A.

y = 2 x + 1

B.

y = 2 x - 1

C.

y = - 2 x - 3

D.

y = - 2 x - 2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 如图, 质点

P

在半径为 2 的圆周上逆时针运动, 其初始位置为

P_{0} (\sqrt{2}

- \sqrt{2}

), 角速度为 1 , 那么点

P

到

x

轴距离

d

关于时间

t

的函数图象大致为（　　）

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 已知命题

p_{1}

：函数

y = 2^{x} - 2^{- x}

在

R

为增函数,

p_{2}

: 函数

y = 2^{x} + 2^{- x}

在

R

为减函数, 则在命题

q_{1} : p_{1} \lor p_{2}, q_{2} : p_{1} \land p_{2}, q_{3} : (\neg p_{1}) \lor p_{2}

和

q_{4} : p_{1} \land (\neg

p_{2}

）中, 真命题是（）

A.

q_{1}, q_{3}

B.

q_{2}, q_{3}

C.

q_{1}, q_{4}

D.

q_{2}, q_{4}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 某种种子每粒发芽的概率都为

0.9

, 现播种了 1000 粒, 对于没有发芽的种子, 每粒需再补种 2 粒, 补种的种子数记为

X

, 则

X

的数学期望为 ( )

A.

100

B.

200

C.

300

D.

400

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

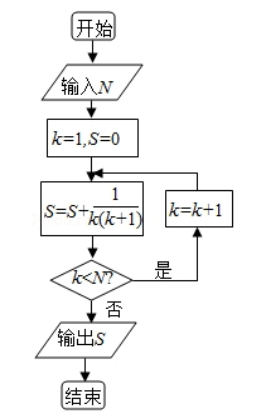
7. 如果执行如图的框图，输入 N=5，则输出的数等于（）

A.

\frac{5}{4}

B.

\frac{4}{5}

C.

\frac{6}{5}

D.

\frac{5}{6}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 设偶函数

f (x)

满足

f (x) = 2^{x} - 4 (x ⩾ 0)

，则

{x ∣ f (x - 2) > 0} =

（　　）

A.

{x ∣ x < - 2

或

x > 4}

B.

{x ∣ x < 0

或

x > 4}

C.

{x ∣ x < 0

或

x > 6}

D.

{x ∣ x < - 2

或

x > 2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 若

\cos α = - \frac{4}{5}, α

是第三象限的角, 则

\frac{1 + \tan \frac{α}{2}}{1 - \tan \frac{α}{2}} =

（　　）

A.

- \frac{1}{2}

B.

\frac{1}{2}

C.

2

D.

- 2

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 设三棱柱的侧棱垂直于底面, 所有棱长都为

a

, 顶点都在一个球面上, 则该球的表面积为（　　）

A.

π a^{2}

B.

\frac{7}{3} π a^{2}

C.

\frac{11}{3} π a^{2}

D.

5 π a^{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知函数

f (x) = {\begin{cases} | lgx |, 0 < x ⩽ 10 \\ - \frac{1}{2} x + 6, x > 10 \end{cases}

, 若

a, b, c

互不相等, 且

f (a)

= f (b) = f (c)

, 则

a b c

的取值范围是（　　）

A.

(1, 10)

B.

(5, 6)

C.

(10, 12)

D.

(20, 24)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 已知双曲线

E

的中心为原点,

P (3, 0)

是

E

的焦点, 过

P

的直线

I

与

E

相交于

A, B

两点, 且

A B

的中点为

N (- 12, - 15)

, 则

E

的方程式为（ )

A.

\frac{x^{2}}{3} - \frac{y^{2}}{6} = 1

B.

\frac{x^{2}}{4} - \frac{y^{2}}{5} = 1

C.

\frac{x^{2}}{6} - \frac{y^{2}}{3} = 1

D.

\frac{x^{2}}{5} - \frac{y^{2}}{4} = 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 4 题），请把答案直接填写在答题纸上

13. 设

y = f (x)

为区间

[0, 1]

上的连续函数, 且恒有

0 ⩽ f (x) ⩽ 1

, 可以用随机模拟方法近似计算积分

\int_{0}^{1} f (x) dx

, 先产生两组 (每组

N

个) 区间 [0, 1] 上的均匀随机数

x_{1}, x_{2}, \dots x_{N}

和

y_{1}, y_{2}, \dots y_{N}

, 由此得到

N

个点

(x_{i}, y_{i})

(

i = 1, 2, \dots, N)

, 再数出其中满足

y_{i} ⩽ f (x_{i}) (i = 1, 2, \dots, N)

的点数

N_{1}

, 那么由随机模拟方案可得积分

\int_{0}^{1} f (x) d x

的近似值为（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 正视图为一个三角形的几何体可以是（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 过点

A (4, 1)

的圆

C

与直线

x - y = 1

相切于点

B (2, 1)

, 则圆

C

的方程为（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 在

△ A B C

中,

D

为边

B C

上一点,

B D = \frac{1}{2} D C, ∠ A D B = 120^{\circ}, A D = 2

, 若

△

A D C

的面积为

3 - \sqrt{3}

, 则

∠ B A C =

（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 8 题），解答过程应写出必要的文字说明、证明过程或演算步骤

17. 设数列满足

a_{1} = 2, a_{n + 1} - a_{n} = 3 \cdot 2^{2 n - 1}

（1）求数列

{a_{n}}

的通项公式;
(2) 令

b_{n} = n a_{n}

, 求数列

{b_{n}}

的前

n

项和

S_{n}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

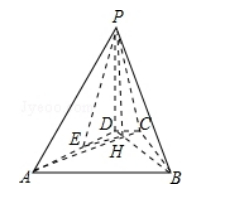
18. 如图, 已知四棱雉

P - A B C D

的底面为等腰梯形,

A B / / C D, A C ⊥ B D

, 垂足为

H, PH

是四棱雉的高,

E

为

AD

中点
(I ) 证明:

P E ⊥ B C

(II ) 若

∠ APB = ∠ ADB = 60^{\circ}

, 求直线

P A

与平面

PEH

所成角的正弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样
方法从该地区调查了 500 位老年人，结果如表：

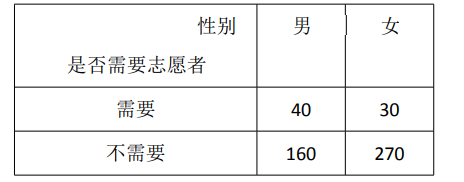
（1）估计该地区老年人中，需要志愿者提供帮助的比例；
（2）能否有 99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有
关？
（3）根据（2）的结论，能否提出更好的调查方法来估计该地区的老年人中需要
志愿者提供帮助的老年人比例？说明理由．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 设

F_{1}, F_{2}

分别是椭圆

E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)

的左、右焦点, 过

F_{1}

斜率为 1 的直线

ℓ

与

E

相交于

A, B

两点, 且

| A F_{2} |, | A B |, | B_{2} |

成等差数列
(1) 求

E

的离心率;
(2) 设点

P (0, - 1)

满足

| P A | = | P B |

, 求

E

的方程.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 设函数

f (x) = e^{x} - 1 - x^{-} a x^{2}

.
（1）若

a = 0

, 求

f (x)

的单调区间;
（2）若当

x ⩾ 0

时

f (x) ⩾ 0

, 求

a

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

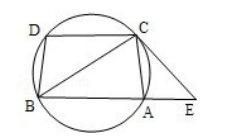
22. 如图: 已知圆上的弧

\hat{A C} = \hat{B D}

, 过

C

点的圆的切线与

B A

的延长线交
于

E

点, 证明:
(I)

∠ ACE = ∠ BCD

.
(II )

{BC}^{2} = BE \cdot CD

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 已知直线

C_{1} {\begin{cases} x = 1 + t \cos α \\ y = t \sin α \end{cases}

(t 为参数) ,

C_{2} {\begin{cases} x = \cos θ \\ y = \sin θ \end{cases}

(

θ

为参数),
（I）当

α = \frac{π}{3}

时, 求

C_{1}

与

C_{2}

的交点坐标;
(II) 过坐标原点

O

做

C_{1}

的垂线, 垂足为

A, P

为

O A

中点, 当

α

变化时, 求

P

点的轨迹的参数方程, 并指出它是什么曲线.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

24. 设函数

f (x) = | 2 x - 4 | + 1

.
(I) 画出函数

y = f (x)

的图象:
(II) 若不等式

f (x) ⩽ a x

的解集非空, 求

a

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。