单选题 (共 10 题 ),每题只有一个选项正确
若 $\frac{|a|}{a-a^2}=\frac{1}{a-1}$, 则 $a$ 的取值范围是
$\text{A.}$ $a>0$ 且 $a \neq 1$
$\text{B.}$ $a \leq 0$
$\text{C.}$ $a \neq 0$ 且 $a \neq 1$
$\text{D.}$ $a < 0$
$\frac{1.3}{1000000000} \times \frac{1.08}{9 \times 10^{16}}$ 用科学记数法表示为 $a \times 10^n$, 其中 $1 \leq a < 10, n$ 为整数, 则 $n=$
$\text{A.}$ -23
$\text{B.}$ -24
$\text{C.}$ -25
$\text{D.}$ -26
分解因式 $x^2+a x+b$ 时, Jagger看错了 $a$ 的值, 分解的结果是 $(x+6)(x-1), M e g$ 看错了 $b$ 的值, 分解的结果是 $(x$ $-2)(x+1)$, 那么正确的分解因式的结果是
$\text{A.}$ $(x+6)(x-2)$
$\text{B.}$ $(x+2)(x-3)$
$\text{C.}$ $(x+6)(x+1)$
$\text{D.}$ $(x-2)(x+3)$
如图, 四边形 $A B C D$ 中, $A C$ 为对角线, 已知 $P 、 Q$ 分别是 $\triangle A B C$ 和 $\triangle A C D$ 内角平分线的交点,若 $\angle A P C+\angle A Q C=250^{\circ}$, 则 $\angle B A D+\angle B C D$ 的值为

$\text{A.}$ $220^{\circ}$
$\text{B.}$ $230^{\circ}$
$\text{C.}$ $240^{\circ}$
$\text{D.}$ $250^{\circ}$
若 $a 、 b$ 为有理数, 且 $\frac{2 \sqrt{3}-b}{3-a \sqrt{3}}=\sqrt{3}+1$, 则 $a 、 b$ 的值分别为
$\text{A.}$ $1 、 0$
$\text{B.}$ $2 、 2$
$\text{C.}$ $4 、 1$
$\text{D.}$ $0 、 2$
015年8月31日慧聪网报道, 爱唱响内蒙音乐夏令营9月开启, 某学校组织部分学生参加夏令营, 李老师从夏令营咨询处带回如图所示的两条信息, 则原来报名参加夏令营的学生有

$\text{A.}$ 100人
$\text{B.}$ 150人
$\text{C.}$ 200人
$\text{D.}$ 250人
如图, $G$ 为 $\triangle A B C$ 的重心, $M 、 N$ 两点分别在 $A B 、 B C$ 上, 且 $G M \perp A B, G N \perp B C$, 若 $A B=12, B C=5, \angle B$ $=90^{\circ}$, 则长方形 $B M G N$ 的面积为

$\text{A.}$ $\frac{26}{3}$
$\text{B.}$ $\frac{20}{3}$
$\text{C.}$ 8
$\text{D.}$ 6
如图, 线段 $A B=C D, A B$ 与 $C D$ 相交于 $O$, 且 $\angle A O C=60^{\circ}, C E$ 是由 $A B$ 平移所得, 则 $A C+B$ $D$ 与 $A B$ 的大小关系是

$\text{A.}$ $A C+B D>A B$
$\text{B.}$ $A C+B D=A B$
$\text{C.}$ $A C+B D < A B$
$\text{D.}$ $A C+B D \geq A B$
如图, 在平行四边形 $A B C D$ 和平行四边形 $B E F G$ 中, $A B=A D, B G=B E$, 点 $A 、 B 、 E$ 在同一直线上, $P$ 是线段 $D F$ 的中点, 连接 $P G, P C$. 若 $\angle A B C=\angle B E F=60^{\circ}$, 则 $\frac{P G}{P C}=$

$\text{A.}$ $\sqrt{2}$
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\frac{\sqrt{2}}{2}$
$\text{D.}$ $\frac{\sqrt{3}}{3}$
如图, 在 $Z$ 小区内的正六边形花园中铺设道路, 如果图中实线表示水泥路, 虚线表示沥青路, 若按方案一铺设, 共需 315 万元; 若按方案二铺设,共需300万元;若按方案三铺设, 则需要

$\text{A.}$ 150 万元
$\text{B.}$ 200 万元
$\text{C.}$ 270 万元
$\text{D.}$ 380 万元
填空题 (共 3 题 ),请把答案直接填写在答题纸上
计算 $123456785 \times 123456782-123456783 \times 123456784$ 的结果为
若 $\left|a-x-\frac{1}{x}\right|+\sqrt{x^2-3+\frac{1}{x^2}}=0$, 那么 $\sqrt{(a-2)^2}$ 等于
如图所示是一条宽为 $1.5 \mathrm{~m}$ 的直角走廊, 现有一辆转动灵活的手推车, 其矩形平板面 $A B C D$ 的宽 $A$ $B$ 为 $1 m$, 若要想顺利推过 (不可坚起来或侧翻) 直角走廊, 平板车的长 $A D$ 不能超过 $m$. ( 精确到 0.1 , 参考数据: $\sqrt{2} \approx 1.41, \sqrt{3} \approx 1.73$ )

解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
高斯符号 $[x]$ 表示不大于 $x$ 的最大整数, 例如: $[3.25]=3,[2.38]=2$, 已知 $a 、 b$ 都是正整数, 且满足 $[1.9 a]+[8.8 b]=$ 30, 则 $a 、 b$ 的值共有几组?
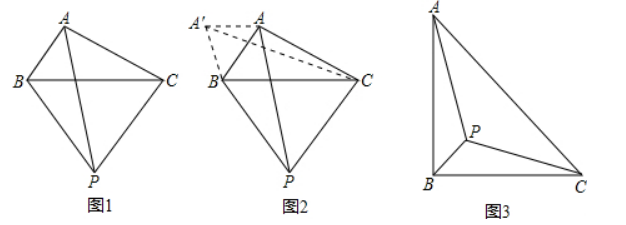
小伟遇到这样一个问题: 如图 1, 在 $\triangle A B C$ (其中 $\angle B A C$ 是一个可以变化的角) 中, $A B=2, A C=4$, 以 $B C$ 为边在 $B C$ 的下方作等边 $\triangle P B C$, 求 $A P$ 的最大值.
小伟是这样思考的: 利用变换和等边三角形将边的位置重新组合. 他的方法是以点 $B$ 为旋转中心将 $\triangle A B P$ 逆时针旋转 $60^{\circ}$ 得到 $\triangle$ $A^{\prime} B C$, 连接 $A^{\prime} A$, 当点 $A$ 落在 $A^{\prime} C$ 上时, 此题可解 (如图2).
请你回答: $A P$ 的最大值是
参考小伟同学思考问题的方法, 解决下列问题:
如图3, 等腰Rt $\triangle A B C$. 边 $A B=4, P$ 为 $\triangle A B C$ 内部一点, 则 $A P+B P+C P$ 的最小值是 . ( 结果可以不化简)