单选题 (共 8 题 ),每题只有一个选项正确
某工厂随机抽取 20 名工人,对他们某天生产的产品件数进行统计,数据如下表,则该组数据的第 75 百分位数是
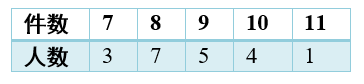
$\text{A.}$ 8.5
$\text{B.}$ 9
$\text{C.}$ 9.5
$\text{D.}$ 10
某学校举办作文比赛,共设 6 个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题的概率为( )
$\text{A.}$ $\frac{5}{6}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{1}{3}$
某运动员每次射击击中目标的概率均相等,若在三次射击中,至少有一次击中目标的概率为 $\frac{63}{64}$ ,则射击一次,击中目标的概率为
$\text{A.}$ $\frac{7}{8}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{8}$
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
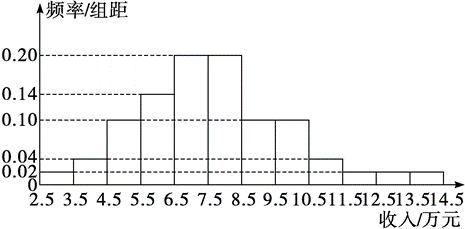
根据此频率分布直方图,下面结论中不正确的是( )
$\text{A.}$ 该地农户家庭年收入低于 4.5 万元的农户比率估计为 $6 \%$
$\text{B.}$ 该地农户家庭年收入不低于 10.5 万元的农户比率估计为 $10 \%$
$\text{C.}$ 估计该地农户家庭年收入的平均值不超过 6.5 万元
$\text{D.}$ 估计该地有一半以上的农户,其家庭年收入介于 4.5 万元至 8.5 万元之间
设某种植园成熟的红橙单果质量 $M$(单位: g )服从正态分布 $N\left(165, \sigma^2\right)$ ,且 $P(M < 162)=0.15, P(165 < M < 167)=0.3$ .下列说法正确的是( )
$\text{A.}$ 若从种植园成熟的红橙中随机选取 1 个,则这个红橙的质量小于 167 g 的概率为 0.7
$\text{B.}$ 若从种植园成熟的红橙中随机选取 1 个,则这个红橙的质量在 $167 \mathrm{~g} \sim 168 \mathrm{~g}$ 之间的概率为 0.05
$\text{C.}$ 若从种植园成熟的红橙中随机选取 600 个,则质量大于 163 g 的个数的数学期望为 480
$\text{D.}$ 若从种植园成熟的红橙中随机选取 600 个,则质量在 $163 \mathrm{~g} \sim 168 \mathrm{~g}$ 之间的个数的方差为 136.5
有 3 台车床加工同一型号的零件,第 1 台加工的次品率为 $8 \%$ ,第 2 台加工的次品率为 $3 \%$ ,第 3 台加工的次品率为 $2 \%$ ,加工出来的零件混放在一起。已知第 $1,2,3$ 台车床加工的零件数分别占总数的 $10 \%, 40 \%, 50 \%$ ,从混放的零件中任取一个零件,则下列结论正确的是
$\text{A.}$ 该零件是第 1 台车床加工出来的次品的概率为 0.08
$\text{B.}$ 该零件是次品的概率为 0.03
$\text{C.}$ 如果该零件是第 3 台车床加工出来的,那么它不是次品的概率为 0.98
$\text{D.}$ 如果该零件是次品,那么它不是第 3 台车床加工出来的概率为 $\frac{1}{3}$
甲箱中有 4 个红球、 2 个白球和 3 个黑球,乙箱中有 3 个红球、 3 个白球和 3 个黑球,先从甲箱中随机取出一球放入乙箱,分别以 $A_1, A_2$ 和 $A_3$ 表示事件由甲箱取出的球是红球、白球和黑球;再从乙箱中随机取出一球,以 $B$ 表示事件由乙箱取出的球是红球,则下列结论正确的是
$\text{A.}$ 事件 $B$ 与事件 $A_i(i=1,2,3)$ 相互独立
$\text{B.}$ $P\left(A_1 B\right)=\frac{8}{45}$
$\text{C.}$ $P(B)=\frac{1}{3}$
$\text{D.}$ $P\left(A_2 \mid B\right)=\frac{6}{31}$
现有甲、乙、丙三位篮球运动员连续 5 场篮球比赛得分情况的记录数据,已知三位球员得分情况的数据满足以下条件:
甲球员: 5 个数据的中位数是 26 ,众数是 24 ;
乙球员: 5 个数据的中位数是 29 ,平均数是 26 ;
丙球员: 5 个数据有 1 个是 32 ,平均数是 26 ,方差是 9.6 .
根据以上统计数据,下列统计结论一定正确的是
$\text{A.}$ 甲球员连续 5 场比赛得分都不低于 24 分
$\text{B.}$ 乙球员连续 5 场比赛得分都不低于 24 分
$\text{C.}$ 丙球员连续 5 场比赛得分都不低于 24 分
$\text{D.}$ 丙球员连续 5 场比赛得分的第 60 百分位数大于 24
多选题 (共 1 题 ),每题有多个选项正确
已知事件 $A, B$ 满足 $P(A)=0.5, P(B)=0.2$ ,则( )
$\text{A.}$ 若 $B \subseteq A$ ,则 $P(A B)=0.5$
$\text{B.}$ 若 $A$ 与 $B$ 互斥,则 $P(A+B)=0.7$
$\text{C.}$ 若 $A$ 与 $B$ 相互独立,则 $P(A \bar{B})=0.9$
$\text{D.}$ 若 $P(B \mid A)=0.2$ ,则 $A$ 与 $B$ 相互独立
填空题 (共 5 题 ),请把答案直接填写在答题纸上
一个数学兴趣小组共有 2 名男生 3 名女生,从中随机选出 2 名参加交流会,在已知选出的 2 名中有 1 名是男生的条件下,另 1 名是女生的概率为
某产品的质量检验过程依次为进货检验(IQC)、生产过程检验(IPQC)、出货检验(OQC)三个环节。已知某产品 IQC 的单独通过率为 $\frac{4}{5}, \mathrm{IPQC}$ 的单独通过率为 $\frac{3}{4}$ ,规定上一类检验不通过则不进入下一类检验,未通过可修复后再检验一次(修复后无需从头检验,通过率不变且每类检验最多两次),且各类检验间相互独立,则一件该产品能进入 OQC 环节的概率为
有两台车床加工同一型号的零件,第一台车床加工的优秀率为 $15 \%$ ,第二台车床加工的优秀率为 $10 \%$ .假定两台车床加工的优秀率互不影响,则两台车床加工零件,同时出现优秀品的概率为 $\_\_\_\_$ ;若把加工出来的零件混放在一起,已知第一台车床加工的零件数占总数的 $60 \%$ ,第二台车床加工的零件数占总数的 $40 \%$ ,现任取一个零件,则它是优秀品的概率为 $\_\_\_\_$ .
某班共有 50 名学生,在期末考试中,小明因病未参加数学考试,参加考试的 49名学生的数学成绩的方差为 2 。在评估数学成绩时,老师把小明的数学成绩按这 49 名学生的数学成绩的平均数来算,那么全班 50 名学生的数学成绩的标准差为
某校采用分层随机抽样的方法采集了高一、高二、高三年级学生的身高情况,部分调查数据如下:
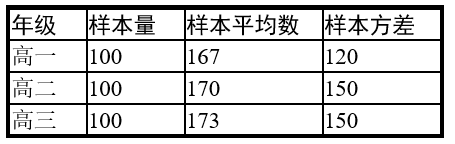
则总样本的方差 $s^2=$