单选题 (共 10 题 ),每题只有一个选项正确
如图为 2017-2021年上海市货物进出口总额的条形统计图,则下列对于进出口贸易额描述错误的是( )
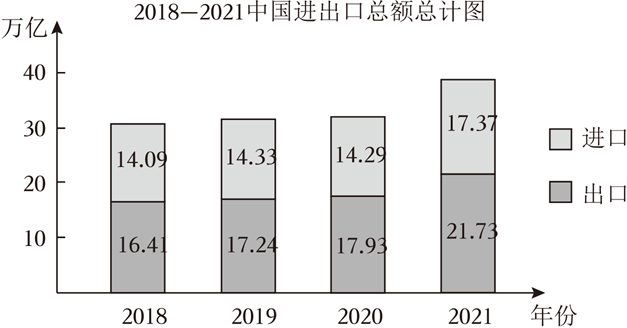
$\text{A.}$ 从2018年开始,2021年的进出口总额增长率最大
$\text{B.}$ 从2018年开始,进出口总额逐年增大
$\text{C.}$ 从2018年开始,进口总额逐年增大
$\text{D.}$ 从 2018 年开始,2020年的进出口总额增长率最小
为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:$k P a$ )的分组区间为 $[12,13),[13,14),[14,15),[15,16),[16,17]$ ,将其按从左到右的顺序分别编号为第一组,第二组,$\ldots$ ,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有 20 人,第三组中没有疗效的有 6 人,则第三组中有疗效的人数为( )
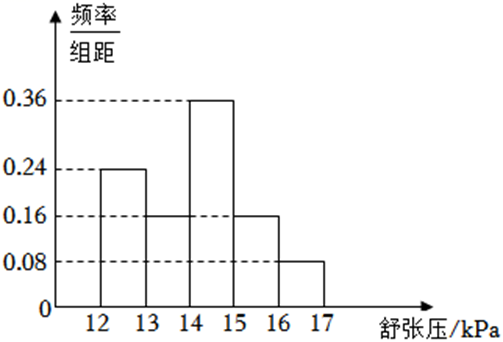
$\text{A.}$ 8
$\text{B.}$ 12
$\text{C.}$ 16
$\text{D.}$ 18
已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层随机抽样的方法抽取2%的学生进行调查,则样本量和抽取的高中生近视人数分别为
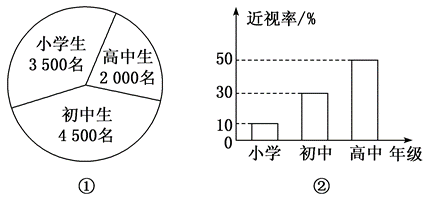
$\text{A.}$ 200,20
$\text{B.}$ 100,20
$\text{C.}$ 200,10
$\text{D.}$ 100,10
给定一组数据 $5,5,4,3,3,3,2,2,2,1$ ,则这组数据())
$\text{A.}$ 众数为 2
$\text{B.}$ 平均数为 2.5
$\text{C.}$ 方差为 1.6
$\text{D.}$ 标准差为 4
下下列抽样方法是简单随机抽样的是( )
$\text{A.}$ 质检员从 50 个零件中一次性抽取 5 个做质量检验
$\text{B.}$ "隔空不隔爱,停课不停学",网课上,李老师对全班 45 名学生中点名表扬了 3 名发言积极的
$\text{C.}$ 老师要求学生从实数集中逐个抽取 10 个分析奇偶性
$\text{D.}$ 某运动员从 8 条跑道中随机抽取一条跑道试跑
酒后驾驶是严重危害交通安全的行为,某交通管理部门对辖区内四个地区(甲、乙、丙、丁)的酒驾治理情况进行检查督导,若"连续 8 天,每天查获的酒驾人数不超过 10 ",则认为"该地区酒驾治理达标",根据连续 8 天检查所得数据的数字特征推断,酒驾治理一定达标的地区是( )
$\text{A.}$ 甲地,均值为 4 ,中位数为 5
$\text{B.}$ 乙地:众数为 3 ,中位数为 2
$\text{C.}$ 丙地:均值为 7 ,方差为 2
$\text{D.}$ 丁地:极差为 $3,75 \%$ 分位数为 8
某年的足球联赛上,甲队每场比赛平均失球数是 1.5 个,全年比赛失球个数的标准差为 1.4 ;乙队每场比赛平均失球数是 2.3 个,全年比赛失球个数的标准差为 0.3 ,下列说法正确的是( )
$\text{A.}$ 甲乙两队相比,乙队很少失球
$\text{B.}$ 甲队比乙队技术水平更稳定
$\text{C.}$ 平均来说,甲队比乙队防守技术好
$\text{D.}$ 乙队有时表现很差,有时表现又非常好
甲同学投掷骰子 5 次,并请乙同学将向上的点数记录下来,计算出平均数和方差.由于记录遗失,乙同学只记得这五个点数的平均数为 2 ,方差在区间 $[1.2,2.4]$ 内,则这五个点数( )
$\text{A.}$ 众数可能为 1
$\text{B.}$ 中位数可能为 3
$\text{C.}$ 一定不会出现 6
$\text{D.}$ 出现 2 的次数不会超过两次
如图是民航部门统计的2026年春运期间十二个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是
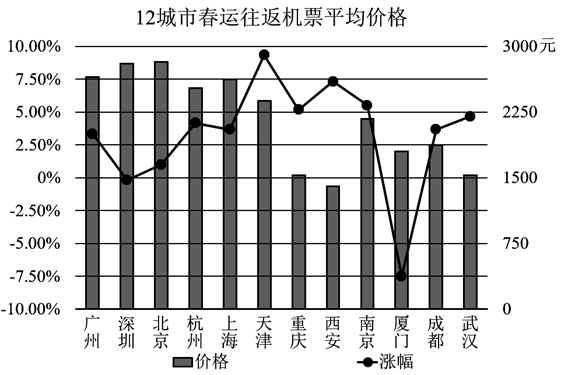
$\text{A.}$ 深圳的变化幅度最小,北京的平均价格最高
$\text{B.}$ 深圳和厦门的春运期间往返机票价格同去年相比有所下降
$\text{C.}$ 平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门
$\text{D.}$ 平均价格从高到低居于前三位的城市为北京、深圳、广州
为了增强大学生的环保意识,加强对"碳中和"概念的宣传,某公益组织分别在 $A, B$ 两所大学随机选取 10 名学生进行环保问题测试(满分 100 分),这 20 名学生得分的折线图如图所示,关于这两所学校被选取的学生的得分,下列结论错误的是( )

$\text{A.}$ A校学生分数的平均分大于 $B$ 校学生分数的平均分
$\text{B.}$ A校学生分数的众数大于 $B$ 校学生分数的众数
$\text{C.}$ A校学生分数的中位数等于 $B$ 校学生分数的中位数
$\text{D.}$ A 校学生分数的方差大于 $B$ 校学生分数的方
多选题 (共 6 题 ),每题有多个选项正确
有一组样本数据 $x_1, x_2, ..., x_6$ ,其中 $x_1$ 是最小值,$x_6$ 是最大值,则()
$\text{A.}$ $x_2, x_3, x_4, x_5$ 的平均数等于 $x_1, x_2, L, x_6$ 的平均数
$\text{B.}$ $x_2, x_3, x_4, x_5$ 的中位数等于 $x_1, x_2, L, x_6$ 的中位数
$\text{C.}$ $x_2, x_3, x_4, x_5$ 的标准差不小于 $x_1, x_2, L, x_6$ 的标准差
$\text{D.}$ $x_2, x_3, x_4, x_5$ 的极差不大于 $x_1, x_2, L, x_6$ 的极差
下列统计量中,能度量样本 $x_1, x_2, \ldots, x_n$ 的离散程度的有
$\text{A.}$ 样本 $x_1, x_2, \ldots, x_n$ 的标准差
$\text{B.}$ 样本 $x_1, x_2, \ldots, x_n$ 的中位数
$\text{C.}$ 样本 $x_1, x_2, \ldots, x_n$ 的极差
$\text{D.}$ 样本 $x_1, x_2, \ldots, x_n$ 的平均数
有一组样本数据 $x_1, x_2, \ldots, x_n$ ,由这组数据得到新样本数据 $y_1, y_2, \ldots, y_n$ ,其中 $y_i=x_i+c(i=1,2$ , $\cdots, n), c$ 为非零常数,则 ()
$\text{A.}$ 两组样本数据的样本平均数相同
$\text{B.}$ 两组样本数据的样本中位数相同
$\text{C.}$ 两组样本数据的样本标准差相同
$\text{D.}$ 两组样本数据的样本极差相同
某中学为了解学生数学史知识的积累情况,随机抽取 150 名同学参加数学史知识测试,测试题共 5 道,每答对一题得 20 分,答错得 0 分.得分不少于 60 分记为及格,不少于 80 分记为优秀,测试成绩百分比分布图如图所示,则( )
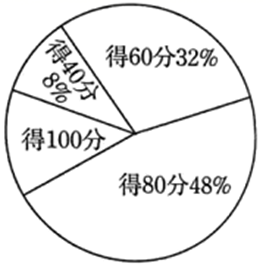
$\text{A.}$ 该次数学史知识测试及格率超过 $90 \%$
$\text{B.}$ 该次数学史知识测试得满分的同学有 15 名
$\text{C.}$ 该次测试成绩的中位数大于测试成绩的平均数
$\text{D.}$ 若该校共有 1500 名学生,则数学史知识测试成绩能得优秀的同学大约有 720 名
某学校组织了一次劳动技能大赛,共有 100 名学生参赛,经过评判,这 100 名参赛者的得分都在[ 40,90 ]内,得分 60 分以下为不及格,其得分的频率分布直方图如图所示(按得分分成$[40,50),[50,60),[60,70),[70,80),[80,90]$ 这五组),则下列结论正确的是( )
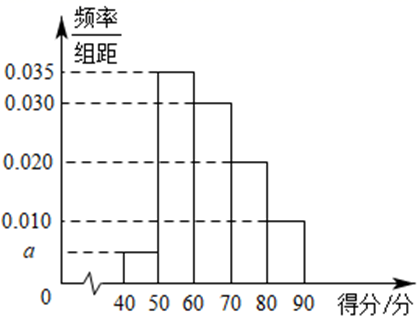
$\text{A.}$ 直方图中 $a=0.005$
$\text{B.}$ 此次比赛得分不及格的共有 40 人
$\text{C.}$ 以频率为概率,从这 100 名参赛者中随机选取 1 人,其得分在 $[60,80)$ 的概率为 0.5
$\text{D.}$ 这 100 名参赛者得分的中位数为 65
气象意义上从春季进入夏季的标志为"当且仅当连续 5 天每天日平均温度不低于 $22^{\circ} C$".现有甲、乙、丙三地连续 5 天日平均温度的记录数据(数据均为正整数,单位 ${ }^{\circ} C$ )且满足以下条件:
甲地: 5 个数据的中位数是 24 ,众数是 22 ;
乙地: 5 个数据的中位数是 27 ,平均数是 24 ;
丙地: 5 个数据有 1 个是 30 ,平均数是 24 ,方差是 9.6 ;
根据以上数据,下列统计结论正确的是( )
$\text{A.}$ 甲地进入了夏季
$\text{B.}$ 乙地进入了夏季
$\text{C.}$ 不能确定丙地进入了夏季
$\text{D.}$ 恰有 2 地确定进入了夏季
填空题 (共 3 题 ),请把答案直接填写在答题纸上
现有某地一年四个季度的 $G D P$(亿元),第一季度 $G D P$ 为 232 (亿元),第四季度 $G D P$ 为 241 (亿元),四个季度的 GDP 逐季度增长,且中位数与平均数相同,则该地一年的 GDP 为
某校抽取 100 名学生测身高,其中身高最大值为 186 cm ,最小值为 154 cm ,根据身高数据绘制频率组距分布直方图,组距为 5 ,且第一组下限为 153.5 ,则组数为
要考察某种品牌的850颗种子的发芽率,从中抽取50颗种子进行实验,利用随机数表法抽取种子,先将850颗种子按001,002,…,850进行编号,如果从随机数表第3行第6列的数开始向右读,请依次写出最先检验的4颗种子的编号: .
注:下面抽取了随机数表第1行至第5行.
03 47 43 73 86 36 96 47 36 61 46 98 63 71 62
33 26 16 80 45 60 11 14 10 95
97 74 24 67 62 42 81 14 57 20 42 53 32 37 32
27 07 36 07 51 24 51 79 89 73
16 76 62 27 66 56 50 26 71 07 32 90 79 78 53
13 55 38 58 59 88 97 54 14 10
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15
57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90
06 18 44 32 53 23 83 01 30 30