单选题 （共 10 题 ），每题只有一个选项正确
一个非零的复数 $z$ 乘以 $-i$ ，则相当于（ ）．
$\text{A.}$ 将复数 $z$ 逆时针旋转 $\frac{\pi}{2}$
$\text{B.}$ 将复数 $z$ 顺时针旋转 $\frac{\pi}{2}$
$\text{C.}$ 将复数 $z$ 顺时针旋转 $\frac{3 \pi}{2}$
$\text{D.}$ 将复数 $z$ 逆时针旋转 $\pi$
若规定幅角主值 $\arg z \in[0,2 \pi)$ ，则 $\arg \left[(\sqrt{3}+i)^{-3}\right]$ 为（） ．
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{3 \pi}{4}$
$\text{C.}$ $\frac{3 \pi}{2}$
$\text{D.}$ $\frac{5 \pi}{4}$
设 $f(z)=\frac{1+z}{1-z}$ ，则当 $|z| < 1$ 时有（ ）．
$\text{A.}$ $\operatorname{Re} f(x)>0$
$\text{B.}$ $\quad \operatorname{Re} f(x) < 0$
$\text{C.}$ $\operatorname{Im} f(z)>0$
$\text{D.}$ $\operatorname{Im} f(z) < 0$
复数 $z=-3\left(\cos \frac{4}{5} \pi-i \sin \frac{4}{5} \pi\right)$ 的三角表示式为
$\text{A.}$ $\quad 3\left(\cos \frac{4}{5} \pi+i \sin \frac{4}{5} \pi\right)$
$\text{B.}$ $\quad 3\left(\cos \frac{\pi}{5}-i \sin \frac{\pi}{5}\right)$
$\text{C.}$ $\quad 3\left(\cos \frac{4}{5} \pi-i \sin \frac{4}{5} \pi\right)$
$\text{D.}$ $\quad 3\left(\cos \frac{\pi}{5}+i \sin \frac{\pi}{5}\right)$
设 $W_0=\sqrt[8]{2}\left(\cos \frac{\pi}{16}+i \sin \frac{\pi}{16}\right)$ ，则 $1+i$ 的四次方根为
$\text{A.}$ $\quad w_0, 2 w_0, 3 w_0, 4 w_0$
$\text{B.}$ $W_0, W_0^2, W_0^3, W_0^4$
$\text{C.}$ $\quad w_0, i w_0, i^2 w_0, i^3 w_0$
$\text{D.}$ $\quad w_0, i w_0,-i^2 w_0,-i^3 w_0$
在球极射影下，$x O y$ 平面上的点 $\sqrt{3}$ 在球面上的像点为 () ．
$\text{A.}$ $\left(\frac{\sqrt{3}}{2}, 0, \frac{1}{2}\right)$
$\text{B.}$ $\left(\frac{\sqrt{3}}{2}, \frac{1}{2}, 0\right)$
$\text{C.}$ $\left(\frac{\sqrt{3}}{2}, 0,-\frac{1}{2}\right)$
$\text{D.}$ $\left(\frac{\sqrt{3}}{2},-\frac{1}{2}, 0\right)$
满足条件 $\left|\frac{z-1}{z-i}\right|>1$ 的 $z$ 之集合表示复平面上的（ ）．
$\text{A.}$ 有界单连通区域
$\text{B.}$ 有界多连通区域
$\text{C.}$ 无界单连通区域
$\text{D.}$ 无界多连通区域
下列不等式表示的复平面点集中，既不是开集也不是闭集的集合是（ ）。
$\text{A.}$ $\operatorname{Im} z>0$
$\text{B.}$ $\operatorname{Im} z=1$
$\text{C.}$ $0 \leq \arg z \leq \frac{\pi}{4}$
$\text{D.}$ $|z-4| \geq|z|$
设 $z_1, z_2$ 为复常数，$\lambda>0$ 且 $\lambda \neq 1$ ，则满足条件 $\left|\frac{z-z_1}{z-z_2}\right|=\lambda$ 的 $z$ 之集合表示复平面上的 （ ）．
$\text{A.}$ 直线
$\text{B.}$ 圆周
$\text{C.}$ 抛物线
$\text{D.}$ 双曲线
满足不等式 $|z-2|-|z+2|>3$ 的复数 $z$ 表示的平面点集所对应的阴影图形是
$\text{A.}$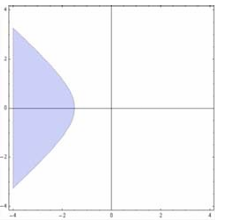 
$\text{B.}$ 
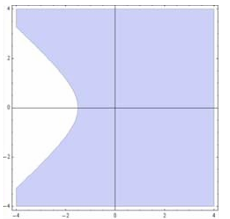$\text{C.}$ 
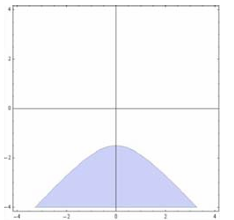$\text{D.}$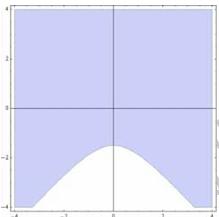 
判断题 （共 11 题 ）
两个复数乘积的幅角主值等于它们的幅角主值的和
$\text{A.}$ 正确
$\text{B.}$ 错误
满足方程 $|z+i|+|z-i|=6$ 的复数 $z$ 构成的平面点集为椭圆
$\text{A.}$ 正确
$\text{B.}$ 错误
$\sin \frac{\pi}{3}-i \cos \frac{\pi}{3}$ 的三角表示为 $\cos \left(-\frac{\pi}{6}\right)+i \sin \left(-\frac{\pi}{6}\right)$ ．
$\text{A.}$ 正确
$\text{B.}$ 错误
若互不相同的复数 $Z_1, Z_2, Z_3$ 满足 $Z_1+Z_2+Z_3=0$ ，则它们一定为正三角形的三个顶点．
$\text{A.}$ 正确
$\text{B.}$ 错误
在球极射影下，$x O y$ 平面上的圆 $|z|=1$ 上的点不变．
$\text{A.}$ 正确
$\text{B.}$ 错误
点集 $E$ 的聚点一定是 $E$ 中的点．
$\text{A.}$ 正确
$\text{B.}$ 错误
集合 $E=\{z|z \in C ,|z+2|-|z-2|>1\}$ 是有界区域
$\text{A.}$ 正确
$\text{B.}$ 错误
点集 $E=\{z \mid z \in C , \operatorname{Re}(z+i \bar{z})>0\}$ 是单连通区域．
$\text{A.}$ 正确
$\text{B.}$ 错误
曲线 $C: z(t)=\left(t^2+1\right)+i t^3(-1 \leq t \leq 1)$ 为光滑闭曲线
$\text{A.}$ 正确
$\text{B.}$ 错误
点集 $E=\{z|z \in C , 1 < |z| \leq 2\}$ 的边界为圆周 $\{z|z \in C ,|z|=2\}$
$\text{A.}$ 正确
$\text{B.}$ 错误
点集 $E=\{z \mid z \in C , \bar{z} \bar{z}-(2+i) z-(2-i) \bar{z} < 4\}$ 是半径为 2 的开圆盘
$\text{A.}$ 正确
$\text{B.}$ 错误
填空题 （共 4 题 ），请把答案直接填写在答题纸上
当 $z=i$ 时， $\operatorname{Re}\left(\frac{z^2+\bar{z} \bar{z}-2}{z-1}\right)$ 的值为 $\qquad$ ．
当 $z=\frac{1+i}{1-i}$ 时，$\left|z^{2017}+z^{2018}+z^{2019}\right|$ 的值为
$\operatorname{Im}(1-i)^4$ 的值为
复数 $(1+\sqrt{3} i)^3$ 的值为