单选题 (共 11 题 ),每题只有一个选项正确
从 2 至 8 的 7 个整数中随机取 2 个不同的数,则这 2 个数互质的概率为
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
将 3 个 1 和 2 个 0 随机排成一行,则 2 个 0 不相邻的概率为
$\text{A.}$ . 0.3
$\text{B.}$ 0.5
$\text{C.}$ 0.6
$\text{D.}$ 0.8
我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果 哥德巴赫猜想是"每个大于 2 的偶数可以表示为两个素数的和",如 $30=7+23$ 。在不超过 30 的素数中,随机选取两个不同的数,其和等于 30 的概率是
$\text{A.}$ $\frac{1}{12}$
$\text{B.}$ $\frac{1}{14}$
$\text{C.}$ $\frac{1}{15}$
$\text{D.}$ $\frac{1}{18}$
我国古代典籍《周易》用"卦"描述万物的变化.每一"重卦"由从下到上排列的 6 个爻组成,爻分为阳爻"——"和阴爻"——",右图就是一重卦。在所有重卦中随机取一重卦,则该重卦恰有 3 个阳爻的概率是()
$\text{A.}$ $\frac{5}{16}$
$\text{B.}$ $\frac{11}{32}$
$\text{C.}$ $\frac{21}{32}$
$\text{D.}$ $\frac{11}{16}$
掷两颗均匀的骰子,则点数之和为 5 的概率等于( )
$\text{A.}$ $\frac{1}{18}$
$\text{B.}$ $\frac{1}{9}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{1}{12}$
2019年中国北京世界园艺博览会于4月29日至10月7日在北京市延庆区举办。如果小明从中国馆、国际馆、植物馆、生活体验馆四个展馆中随机选择一个进行参观,那么他选择的展馆恰为中国馆的概率为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{8}$
$\text{D.}$ $\frac{1}{16}$
如果 3 个正整数可作为一个直角三角形三条边的边长,则称这 3 个数为一组勾股数。从 $1,2,3,4,5$ 中任取 3 个不同的数,则这 3 个数构成一组勾股数的概率为
$\text{A.}$ $\frac{1}{10}$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ $\frac{3}{10}$
$\text{D.}$ $\frac{1}{20}$
在一个不透明的容器中有 6 个小球,其中有 4 个黄球, 2 个红球,它们除颜色外完全相同,如果一次随机取出 2 个球,那么至少有 1 个红球的概率为()
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{7}{15}$
$\text{D.}$ $\frac{8}{15}$
两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是()
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
从 $0,2,4,6,8$ 中任取 2 个不同的数分别记作 $a, b$ ,则 $|a-b| \geqslant 3$ 的概率是()
$\text{A.}$ $\frac{1}{5}$
$\text{B.}$ $\frac{3}{10}$
$\text{C.}$ $\frac{2}{5}$
$\text{D.}$ $\frac{3}{5}$
甲、乙、丙三人是某商场的安保人员,根据值班需要甲连续工作 2 天后休息一天,乙连续工作 3 天后休息一天,丙连续工作 4 天后休息一天,已知 3 月 31 日这一天三人均休息,则4月份三人在同一天工作的概率为()
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{11}{30}$
$\text{D.}$ $\frac{3}{10}$
多选题 (共 4 题 ),每题有多个选项正确
有甲、乙两种报纸供市民订阅,记事件 $E$ 为"只订甲报纸",事件 $F$ 为"至少订一种报纸",事件 $G$ 为"至多订一种报纸",事件 $H$ 为"不订甲报纸",事件 $I$ 为"一种报纸也不订",下列命题正确的是
$\text{A.}$ $E$ 与 $G$ 是互斥事件
$\text{B.}$ $F$ 与 $I$ 是互斥事件,且是对立事件
$\text{C.}$ $F$ 与 $G$ 不是互斥事件
$\text{D.}$ $G$ 与 $I$ 是互斥事件
一个人打靶时连续射击两次,甲表示事件"至少有一次中靶",乙表示事件"恰有一次中靶",丙表示事件"两次都中靶",丁表示事件"两次都不中靶",则下列说法中正确的是( )
$\text{A.}$ 甲与乙是互斥事件
$\text{B.}$ 乙与丙是互斥事件
$\text{C.}$ 乙与丁是对立事件
$\text{D.}$ 甲与丁是对立事件
$A, B$ 为随机事件,已知 $P(A)=0.5, P(B)=0.3$ ,下列结论中正确的是( )
$\text{A.}$ .若 $A, B$ 为互斥事件,则 $P(A+B)=0.8 $ .
$\text{B.}$ 若 $A, B$ 为互斥事件,则 $P(\bar{A}+\bar{B})=0.8$
$\text{C.}$ 若 $A, B$ 是相互独立事件,$P(A+B)=0.65$
$\text{D.}$ 若 $P(B \mid A)=0.5$ ,则 $P(B \mid \bar{A})=0.1$
已知事件 $A, B$ 满足 $P(A)=0.3, P(B)=0.6$ ,则
$\text{A.}$ 若 $\subseteq B$ ,则 $P(A B)=0.18$
$\text{B.}$ 若 $A$ 与 $B$ 互斥,则 $P(A+B)=0.9$
$\text{C.}$ 若 $P(A \mid B)=0.1$ ,则 $A$ 与 $B$ 相互独立
$\text{D.}$ 若 $A$ 与 $B$ 相互独立,则 $P(A \bar{B})=0.12$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
为了学习宣传党的二十大精神,某校学生理论宣讲团赴社区宣讲,已知有 4 名男生, 6 名女生,从 10 人中任选 3 人,则恰有 1 名男生 2 名女生的概率为 $\qquad$ .
为了检测学生的身体素质指标,从游泳类 1 项,球类 3 项,田径类 4 项共 8 项项目中随机抽取 4 项进行检测,则每一类都被抽到的概率为 $\qquad$ .
从正方体的 8 个顶点中任选 4 个,则这 4 个点在同一个平面的概率为 $\qquad$ .
甲、乙、丙三个盒子中装有一定数量的黑球和白球,其总数之比为 $5: 4: 6$ .这三个盒子
中黑球占总数的比例分别为 $40 \%, 25 \%, 50 \%$ .现从三个盒子中各取一个球,取到的三个球都是黑球的概率为 $\qquad$ ;将三个盒子混合后任取一个球,是白球的概率为 $\qquad$ .
从一箱产品中随机地抽取一件,设事件 $A=\{$ 抽到一等品 $\}$ ,事件 $B=\{$ 抽到二等品 $\}$ ,事件 $C=\{$ 抽到三等品 $\}$ ,且已知 $P(A)=0.65, P(B)=0.2, P(C)=0.1$ ,则事件"抽到的产品不是一等品"的概率为 $\qquad$ ;
围棋盒子中有多粒黑子和白子,已知从中取出 2 粒都是黑子的概率为 $\frac{1}{7}$ ,都是白子的概率是 $\frac{12}{35}$ ,则从中任意取出 2 粒恰好是同一色的概率是 $\qquad$ .
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
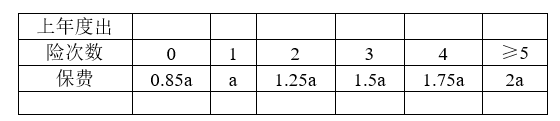
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:

(1)记 A 为事件:"一续保人本年度的保费不高于基本保费",求 $P ( A )$ 的估计值;
(2)记 B 为事件:"一续保人本年度的保费高于基本保费但不高于基本保费的 $160 \%$",求 $P ( B )$ 的估计值;
(3)求续保人本年度平均保费的估计值.
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶 4 元,售价每瓶 6 元,未售出的酸奶降价处理,以每瓶 2 元的价格当天全部处理完。根据往年销售经验,每天需求量与当天最高气温(单位:${ }^{\circ} C$ )有关.如果最高气温不低于 25 ,需求量为 500 瓶;如果最高气温位于区间 $[20,25)$ ,需求量为 300 瓶;如果最高气温低于 20 ,需求量为 200 瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表

以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过 300 瓶的概率;
(2)设六月份一天销售这种酸奶的利润为 $Y$(单位:元).当六月份这种酸奶一天的进货量为 450 瓶时,写出 $Y$ 的所有可能值,并估计 $Y$ 大于零的概率.
先后抛掷两枚质地均匀的骰子,求:
(1) 点数之和是4的倍数的概率;
(2) 点数之和大于5且小于10的概率.
先后抛掷两枚质地均匀的骰子,求:
(1)点数之和出现 7 点的概率;
(2)出现两个 4 点的概率;
(3)点数之和能被 3 整除的概率。