单选题 (共 2 题 ),每题只有一个选项正确
下列可作为数列 $1,2,1,2,1,2, \cdots$ 的通项公式的是( )
$\text{A.}$ $a_{n}=\frac{1+(-1)^{n-1}}{2}$
$\text{B.}$ $a_{n}=\frac{3+(-1)^{n}}{2}$
$\text{C.}$ $a_{n}=2-\sin \frac{n \pi}{2}$
$\text{D.}$ $a_{n}=2-\cos [(n-1) \pi]$
已知数列的通项公式为 $a_{n}=n^{2}-8 n+15$ ,则 3 是数列 $\left\{a_{n}\right\}$ 中的
$\text{A.}$ 第 2 项
$\text{B.}$ 第 6 项
$\text{C.}$ 第 2 项或第 6 项
$\text{D.}$ 第 3 项
多选题 (共 1 题 ),每题有多个选项正确
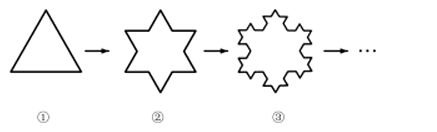
1904年,瑞典数学家科赫构造了一种曲线.如图,取一个边长为 1 的正三角形,在每个边上以中间的 $\frac{1}{3}$ 为一边,向外侧凸出作一个正三角形,再把原来边上中间的 $\frac{1}{3}$ 擦掉,得到第 2 个图形,重复上面的步骤,得到第 3 个图形.这样无限地作下去,得到的图形的轮廓线称为科赫曲线.云层的边缘,山脉的轮廓,海岸线等自然界里的不规则曲线都可用"科赫曲线"的方式来研究,这门学科叫"分形几何学".下列说法正确的是
$\text{A.}$ 第 4 个图形的边长为 $\frac{1}{81}$
$\text{B.}$ 记第 $n$ 个图形的边数为 $a_{n}$ ,则 $a_{n+1}=4 a_{n}$
$\text{C.}$ 记第 $n$ 个图形的周长为 $b_{n}$ ,则 $b_{n}=3 \cdot\left(\frac{4}{3}\right)^{n-1}$
$\text{D.}$ 记第 $n$ 个图形的面积为 $S_{n}$ ,则对任意的 $n \in N^{+}$,存在正实数 $M$ ,使得 $S_{n} < M$
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}=3^{n}-1$ ,求它的通项公式 $a_{n}$ ;
(2)已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}=n^{2}-n$ ,求它的通项公式 $a_{n}$ .
(1)已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}=3^{n}+1$ ,求它的通项公式 $a_{n}$ ;
(2)已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}=n^{2}-n+1$ ,求它的通项公式 $a_{n}$ .
已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和 $S_{n}$ ,求通项 $a_{n}$ .
(1)$S_{n}=3^{n}-1$ ;
(2)$S_{n}=n^{2}+3 n+1$ .