单选题 (共 4 题 ),每题只有一个选项正确
当 $x=1$ 时,函数 $f(x)=a \ln x+\frac{b}{x}$ 取得最大值 -2 ,则 $f^{\prime}(2)=()$
$\text{A.}$ -1
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ 1
已知函数f(x)的导函数的图象如图所示,则f(x)的极值点的个数为
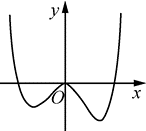
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
已知 $a$ 为函数 $f(x)=x 3-12 x$ 的极小值点,则 $a$ 等于( )
$\text{A.}$ -4
$\text{B.}$ -2
$\text{C.}$ 4
$\text{D.}$ 2
已知 $x=0$ 是函数 $f(x)=e^{a x}-\ln (x+a)$ 的极值点,则 $a=()$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ e
$\text{D.}$ $\pm 1$
多选题 (共 2 题 ),每题有多个选项正确
已知函数 $f(x)=x^3-x+1$ ,则( )
$\text{A.}$ $f(x)$ 有两个极值点
$\text{B.}$ $f(x)$ 有三个零点
$\text{C.}$ 点 $(0,1)$ 是曲线 $y=f(x)$ 的对称中心
$\text{D.}$ 直线 $y=2 x$ 是曲线 $y=f(x)$ 的切线
设函数 $f(x)$ 的定义域为 $R , x_0\left(x_0 \neq 0\right)$ 是 $f(x)$ 的极小值点,以下结论一定正确的是( )
$\text{A.}$ $x_0$ 是 $f(x)$ 的最小值点
$\text{B.}$ $x_0$ 是 $-f(x)$ 的极大值点
$\text{C.}$ $-x_0$ 是 $f(-x)$ 的极大值点
$\text{D.}$ $-x_0$ 是 $-f(-x)$ 的极大值点
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知 $x=x_1$ 和 $x=x_2$ 分别是函数 $f(x)=2 a^x- e x^2(a>0$ 且 $a \neq 1)$ 的极小值点和极大值点.若 $x_1 < x_2$ ,则 $a$ 的取值范围是
已知函数 $f(x)=\frac{1}{2} x-\sin x$ ,则 $f(x)$ 在区间 $[0, \pi]$ 上的值域为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\frac{e^x}{x}-\ln x+x-a$ .
(1)若 $f(x) \geq 0$ ,求 $a$ 的取值范围;
(2)证明:若 $f(x)$ 有两个零点 $x_1, x_2$ ,则环 $x_1 x_2 < 1$ .
已知函数 $f(x)=a x-\frac{1}{x}-(a+1) \ln x$ .
(1)当 $a=0$ 时,求 $f(x)$ 的最大值;
(2)若 $f(x)$ 恰有一个零点,求 $a$ 的取值范围.
已知函数 $f(x)=x^2-1-2 a \ln x(a \neq 0)$ ,求函数 $f(x)$ 的极值.
已知函数 $f(x)=x^3-a x^2+3 x$ ,且 $x=3$ 是 $f(x)$ 的极值点,求函数 $f(x)$ 的极值.
已知函数 $f(x)=x^3-\frac{1}{2} x^2+a x+1$ .
(1)当 $a=2$ 时,求曲线 $y=f(x)$ 在点 $(0, f(0))$ 处的切线方程;
(2)若函数 $f(x)$ 在 $x=1$ 处有极小值,求函数 $f(x)$ 在区间 $\left[-2, \frac{3}{2}\right]$ 上的最大值.
函数 $f(x)=x^3+a x^2+b x+a^2$ 在 $x=1$ 处取得极值 10 ,则 $a+b=$
函数 $f(x)=|x|^{\frac{1}{2}}-\cos x$ 的最小值为