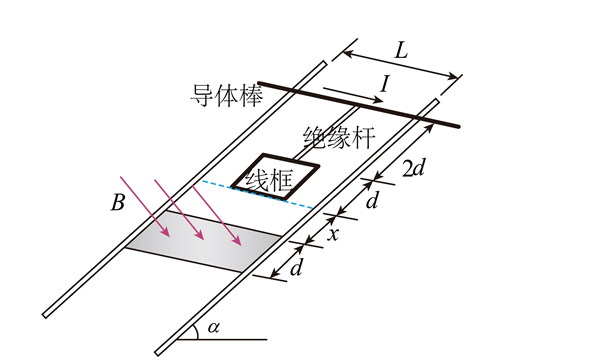
如图所示, 两平行足够长且电阻可忽略的光滑金属导轨安装在倾角为
(1) 装置释放时线框下边与磁场上边界的距离
(2) 若线框下边与磁场区域上边界重合时将线框由静止释放, 导体棒恰好运动到磁场区域 下边界处返回, 求装置从释放到开始返回的过程中, 线框中产生的焦耳热
(3) 在 (2) 情景中求线框第一次穿越磁场区域所需的时间
(1) 装置释放时线框下边与磁场上边界的距离
(2) 若线框下边与磁场区域上边界重合时将线框由静止释放, 导体棒恰好运动到磁场区域 下边界处返回, 求装置从释放到开始返回的过程中, 线框中产生的焦耳热
(3) 在 (2) 情景中求线框第一次穿越磁场区域所需的时间
