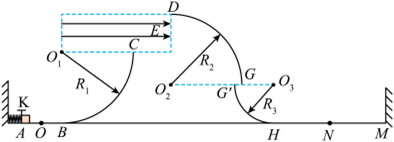
如图为某同学设计的弹射装置, 弹射装置由左端固定在墙上的轻弹簧和锁
(1) 小物块
(2) 电场强度
(3) 小物块
(4) 设小物块
(1) 小物块
(2) 电场强度
(3) 小物块
(4) 设小物块
