如图,四边形
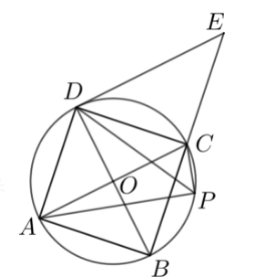
(1)请判断直线
(2)若四边形

(1)请判断直线
(2)若四边形