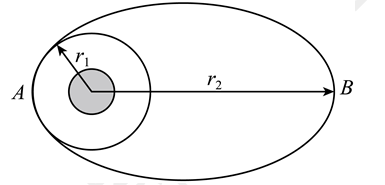
某次发射卫星时, 先将卫星发射到半径为 $r_1$ 的低轨道上, 运行速度为 $v_1$, 当卫星运动经 过 $A$ 点时, 卫星上的小型火箭发动机点火, 短时间加速, 使卫星进入椭圆轨道运行, 椭圆 轨道的远地点 $B$ 与地心的距离为 $r_2$, 卫星经过 $B$ 点的速度为 $v_B$, 其运行轨迹如图所示。若 规定无穷远处引力势能为 0 , 则引力势能的表达式 $E_p=-\frac{G M m}{r}$, 其中 $G$ 为引力常量, $M$ 为 中心天体质量, $m$ 为卫星的质量, $r$ 为两者质心间距, 若卫星运动过程中仅受万有引力作用, 则下列说法正确的是

A. $v_B>v_1$
B. 卫星在椭圆轨道上 $A$ 点的加速度大于 $B$ 点的加速度
C. 卫星在 $A$ 点加速后的速度为 $v_A=\sqrt{\frac{1}{2} G M\left(\frac{1}{r_1}-\frac{1}{r_2}\right)+v_B^2}$
D. 卫星从 $A$ 点运动至 $B$ 点的最短时间为 $t=\frac{1}{v_1} \sqrt{\frac{\left(r_1+r_2\right)^3}{2 r_1}}$