如图, 已知四棱锥 $P-A B C D$ 的底面为菱形, 且 $\angle A B C=60, A B=P C=2, P A=P B=\sqrt{2} . M$ 是 棱 $P D$ 上的点, 且四面体 $M P B C$ 的体积为 $\frac{\sqrt{3}}{6}$.
(1) 证明: $P M=M D$;
(2) 若过点 $C, M$ 的平面 $\alpha$ 与 $B D$ 平行, 且交 $P A$ 于点 $Q$, 求平面 $B C Q$ 与平面 $A B C D$ 夹角的余弦值.
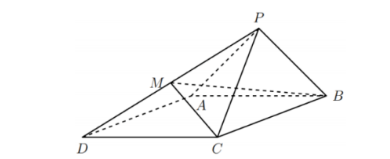
(1) 证明: $P M=M D$;
(2) 若过点 $C, M$ 的平面 $\alpha$ 与 $B D$ 平行, 且交 $P A$ 于点 $Q$, 求平面 $B C Q$ 与平面 $A B C D$ 夹角的余弦值.
