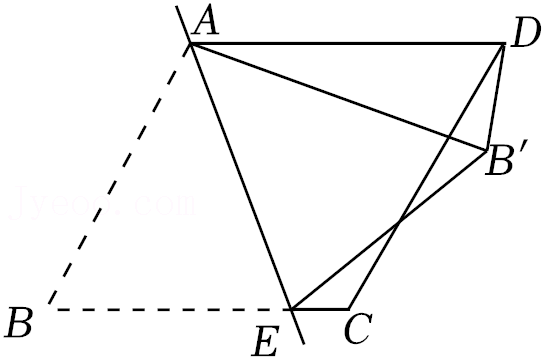
如图, 在菱形纸片 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 是 $\mathrm{BC}$ 边上一点, 将 $\triangle$ $\mathrm{ABE}$ 沿直线 $\mathrm{AE}$ 翻折, 使点 $\mathrm{B}$ 落在 $\mathrm{B}^{\prime}$ 上, 连接 $\mathrm{DB}$ '. 已知 $\angle \mathrm{C}=$ $120^{\circ}, \angle \mathrm{BAE}=50^{\circ}$, 则 $\angle \mathrm{AB}$ 'D 的度数为

A. $50^{\circ}$
B. $60^{\circ}$
C. $80^{\circ}$
D. $90^{\circ}$