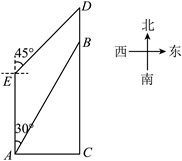
如图, 三角形花园 $A B C$ 紧邻湖泊, 四边形 $A B D E$ 是沿湖泊修建的人行步道. 经测量, 点 $C$ 在点 $\mathrm{A}$ 的 正东方向, $A C=200$ 米. 点 $E$ 在点 $\mathrm{A}$ 的正北方向. 点 $B, D$ 在点 $C$ 的正北方向, $B D=100$ 米. 点 $B$ 在 点 $\mathrm{A}$ 的北偏东 $30^{\circ}$, 点 $D$ 在点 $E$ 的北偏东 $45^{\circ}$.
(1) 求步道 $D E$ 的长度 (精确到个位);
(2) 点 $D$ 处有直饮水, 小红从 $\mathrm{A}$ 出发沿人行步道去取水, 可以经过点 $B$ 到达点 $D$, 也可以经过点 $E$ 到达 点 $D$. 请计算说明他走哪一条路较近? (参考数据: $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732$ )

(1) 求步道 $D E$ 的长度 (精确到个位);
(2) 点 $D$ 处有直饮水, 小红从 $\mathrm{A}$ 出发沿人行步道去取水, 可以经过点 $B$ 到达点 $D$, 也可以经过点 $E$ 到达 点 $D$. 请计算说明他走哪一条路较近? (参考数据: $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732$ )