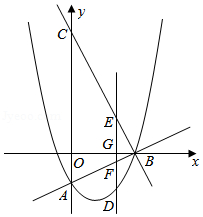
如图, 在平面直角坐标系中, 抛物线 $y=\frac{1}{2} x^{2}+b x+c$ 与坐标轴交 于 $A(0,-2), B(4,0)$ 两点, 直线 $B C: y=-2 x+8$ 交 $y$ 轴于点 $C$. 点 $D$ 为直线 $A B$ 下方抛物线 上一动点, 过点 $D$ 作 $x$ 轴的垂线, 垂足为 $G, D G$ 分别交直线 $B C, A B$ 于点 $E, F$.
（1）求抛物线 $y=\frac{1}{2} x^{2}+b x+c$ 的表达式;
(2) 当 $G F=\frac{1}{2}$ 时, 连接 $B D$, 求 $\triangle B D F$ 的面积;
(3) (1) $H$ 是 $y$ 轴上一点, 当四边形 $B E H F$ 是矩形时, 求点 $H$ 的坐标;
(2)在(1)的条件下, 第一象限有一动点 $P$, 满足 $P H=P C+2$, 求 $\triangle P H B$ 周长的最小值.