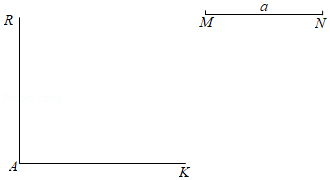如图, 已知线段 $M N=a, A R \perp A K$, 垂足为 $A$.
(1) 求作四边形 $A B C D$, 使得点 $B, D$ 分别在射线 $A K, A R$ 上, 且 $A B=B C=a, \angle A B C$ $=60^{\circ}, C D / / A B$; (要求: 尺规作图, 不写作法, 保留作图痕迹)
(2) 设 $P, Q$ 分别为 (1) 中四边形 $A B C D$ 的边 $A B, C D$ 的中点, 求证: 直线 $A D, B C$, $P Q$ 相交于同一点.