某同学利用如图(a) 所示的实验装置探究物体做直线运动时平均速度与时间的关系。让小车左端和纸带相连。右端用细绳跨过定滑轮和钩码相连。钩码下落，带动小车运动，打点计时器打出纸带。某次实验得到的纸带和相关数据如图(b) 所示。


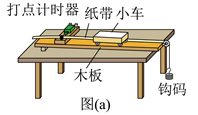
(1)已知打出图(b) 中相邻两个计数点的时间间隔均为 $0.1 \mathrm{~s}$ 以打出A 点时小车位置为初始位置，将打出B、C、D、E、F 各点时小车的位移 $\Delta x$ 填到表中，小车发生应位移所用时间和平均速度分别为 $\Delta t$ 和 $v'$, 表中
$\Delta x_{AD}=$ , $\bar{v_{AD}}= m/s $




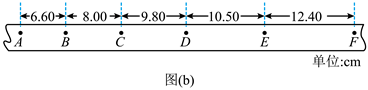
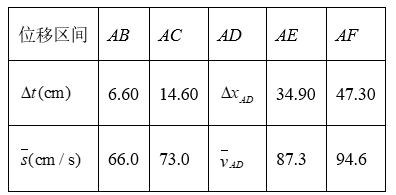
(2)根据表中数据得到小车平均速度 $\bar{v}$ 随时间 $\Delta t$ 的变化关系，如图(c) 所示。 题卡上的图中补全实验点。

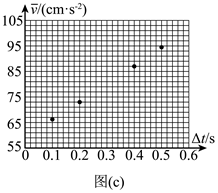
(3)从实验结果可知，小车运动的 $\bar{v}-\Delta t$ 图线可视为一条直线，此直线用方程 $\mathrm{-b}$ 表示，其中 $\mathrm{k}=$ $\mathrm{cm} / \mathrm{s} 2, \mathrm{~b}=$ $\mathrm{cm} / \mathrm{s}$ o (结果均保留3位有效数字)

(4)根据(3)中的直线方程可以判定小车做约加速直线运动，得到打出A 点时小车速度大小VA $=$ 小车的加速度大小 $a=$ 。(结果用字母k、b表示)