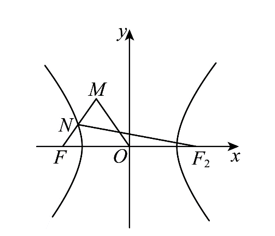
已知 $O$ 是坐标原点, $F$ 是双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点, 平面内一点 $M$ 满足 $\triangle O M F$ 是等边 三角形, 线段 $M F$ 与双曲线 $E$ 交于点 $N$, 且 $|M N|=|N F|$, 则双曲线 $E$ 的离心率为
A
$\frac{\sqrt{13}+1}{3}$
B
$\frac{\sqrt{13}-1}{2}$
C
$\frac{2 \sqrt{15}+2}{7}$
D
$\frac{2 \sqrt{15}+1}{7}$
E
F