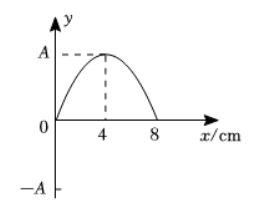
2023年4月山西省高考物理第一轮模拟考试-Kmath科数- 中考、高考、考验数学题库

在研究简谐波的传播时, 波源起振器位于 $O$ 点, 沿 $x$ 轴正方向 $t=0.01 \mathrm{~s}$ 时的波形如图所示。则下列说法正确的是

$ \text{A.}$ 该波的频率为 $100 \mathrm{~Hz}$, 波速为 $8.0 \mathrm{~m} / \mathrm{s}$ $ \text{B.}$ $x=24 \mathrm{~cm}$ 处的质点在 $0.025 \mathrm{~s}$ 时第一次到达波峰的位置 $ \text{C.}$ $x=32 \mathrm{~cm}$ 处的质点在 $\frac{13}{300} s$ 时第一次到达 $\frac{1}{2} A$ 的位置 $ \text{D.}$ $x=48 \mathrm{~cm}$ 处的质点在 $\frac{1}{16} s$ 时第一次到达 $\frac{\sqrt{2}}{2} A$ 的位置

0 人点赞纠错

2 次查看我来讲解

答案：

解析：

解: $A$ 、由图可知, $0.01 \mathrm{~s}$ 内波传播了半个波长, 所用时间是半个周期, 则该波的周期 $T=0.01 s \times 2=0.02 \mathrm{~s}$, 该波的频率为 $f$ $=\frac{1}{T}=\frac{1}{0.02} H z=50 \mathrm{~Hz}$, 波长为 $\lambda=2 \times 8 \times 10^{-2} \mathrm{~m}=0.16 \mathrm{~m}$, 波速为 $v=\frac{\lambda}{T}=\frac{0.16}{0.02} \mathrm{~m} / \mathrm{s}=8 \mathrm{~m} / \mathrm{s}$, 故 $A$ 错误；
$B$ 、波的传播时波形向前平移, $0.01 \mathrm{~s}$ 时波峰在 $x=4 \mathrm{~cm}$ 处, 当 $t=0.01 \mathrm{~s}$ 时 $x=4 \mathrm{~cm}$ 处的波峰第一次传到 $x=24 \mathrm{~cm}$ 处时, $x=2$
$4 \mathrm{~cm}$ 处的质点第一次到达波峰, 则 $x=24 \mathrm{~cm}$ 处的质点第一次到达波峰的位置的时刻为 $t_0=\frac{x_0}{v}=\frac{(24-4) \times 10^{-2}}{8} s+0.01 \mathrm{~s}=0$.
$035 s$,故 $B$ 错误；
$C$ 、由图可知, 该波的起振方向沿 $y$ 轴正方向, 波源的振动方程为 $y=A \sin \left(\frac{2 \pi}{T} t\right)$ 。
波传播到 $x=32 \mathrm{~cm}$ 处的时间 $t_1=\frac{x_1}{v}=\frac{32 \times 10^{-2}}{8} s=0.04 \mathrm{~s}, x=32 \mathrm{~cm}$ 处的质点从起振到达 $\frac{1}{2} A$ 的位置 $\frac{1}{2} A=A \sin \left(\frac{2 \pi}{T} t_2\right)$
解得 $t_2=\frac{T}{12}=\frac{0.02}{12} \mathrm{~s}=\frac{1}{600} \mathrm{~s}, x=32 \mathrm{~cm}$ 处的质点第一次到达 $\frac{1}{2} A$ 位置的时刻 $t=t_1+t_2=0.04 \mathrm{~s}+\frac{1}{600} \mathrm{~s}=\frac{1}{24} \mathrm{~s}$, 故 $C$ 错误；
$D$ 、波传播到 $x=48 \mathrm{~cm}$ 处的时间 $t_3=\frac{x_3}{v}=\frac{48 \times 10^{-2}}{8} s=0.06 \mathrm{~s}, x=48 \mathrm{~cm}$ 处的质点从起振到第一次到达 $\frac{\sqrt{2}}{2} A$ 位置的时间 $\frac{\sqrt{2}}{2} A=\sin \left(\frac{2 \pi}{T} t_4\right)$
解得 $t_4=\frac{T}{8}=\frac{0.02}{8} s=0.0025 \mathrm{~s}, x=48 \mathrm{~cm}$ 处的质点第一次到达 $\frac{\sqrt{2}}{2} A$ 的位置的时刻 $t^{\prime}=t_3+t_4=0.06 \mathrm{~s}+0.0025 \mathrm{~s}=\frac{1}{16} \mathrm{~s}$, 故 $D$ 正确。
故选: D。

关闭页面下载Word格式