在某两个时刻, 太阳光线与地面的夹角分别为 $37^{\circ}$ 和 $45^{\circ}$, 树 $A B$ 长 $6 \mathrm{~m}$.

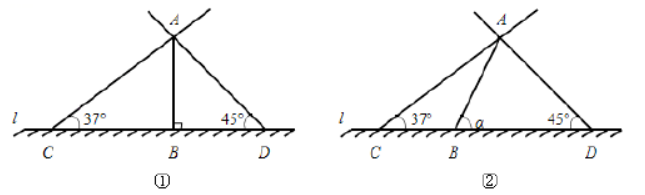
(1)如图①, 若树与地面 $l$ 的夹角为 $90^{\circ}$, 则两次影长的和 $C D=$ m;
(2)如图②, 若树与地面 $l$ 的夹角为 $\alpha$, 求两次影长的和 $C D$ (用含 $\alpha$ 的式子表示).
(参考数据: $\sin 37^{\circ} \approx 0.60, \cos 37^{\circ} \approx 0.80, \tan 37^{\circ} \approx 0.75$ )