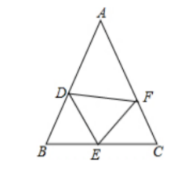
如图, $\triangle \mathrm{ABC}$ 中, $\mathrm{AB}=\mathrm{AC}, D, E, F$ 分别为 $A B, B C, C A$ 上的点, 且 $\mathrm{BD}=\mathrm{CE}$,
$\angle \mathrm{DEF}=\angle B$
(1)求证: $\triangle \mathrm{BDE} \cong \triangle \mathrm{CEF}$;
(2) 若 $\angle A=40^{\circ}$, 求 $\angle E D F$ 的度数.