(1)如图①, 点 $D, E$ 分别在等边 $\triangle \mathrm{ABC}$ 的边 $B C, A B$ 上, 且 $\mathrm{AE}=\mathrm{BD}$, 连接 $A D$, $C E$ 交于点 $F$. 找出图中与 $\triangle \mathrm{ABD}$ 全等的三角形, 证明并求出 $\angle \mathrm{AFE}$ 的度数;



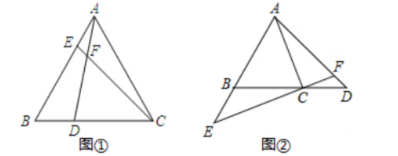
(2) 如图②, 若(1) 中的点 $D, E$ 分别在等边 $\triangle \mathrm{ABC}$ 的边 $B C, A B$ 延长线上, (1)中的结论是否仍然成立? 请说明理由.