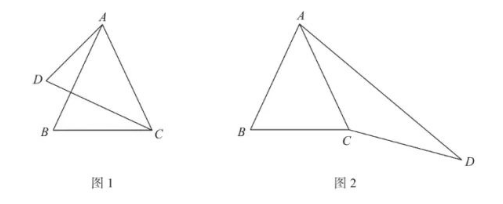
2022年北京市海淀区八年级上学期期末试题-Kmath科数- 中考、高考、考验数学题库

已知在 $\triangle A B C$ 中, $A B=A C$, 且 $\angle B A C=\alpha$. 作 $\triangle A C D$, 使得 $A C=C D$.
(1) 如图 1, 若 $\angle A C D$ 与 $\angle B A C$ 互余, 则 $\angle D C B=$ (用含 $\alpha$ 的代数式表示 );
(2) 如图 2, 若 $\angle A C D$ 与 $\angle B A C$ 互补, 过点 $C$ 作 $C H \perp A D$ 于点 $H$, 求证: $C H=\frac{1}{2} B C$;
(3) 若 $\triangle A B C$ 与 $\triangle A C D$ 的面积相等, 则 $\angle A C D$ 与 $\angle B A C$ 满足什么关系? 请直接写出你的结论.

0 人点赞

24 次查看

我来讲解

答案：

(1) $\frac{\alpha}{2}$.
(2) 取 $B C$ 的中点 $E$, 连接 $A E$.
$\because A B=A C$, 点 $E$ 为 $B C$ 的中点,
$\therefore A E$ 平分 $\angle B A C, A E \perp B C, C E=\frac{1}{2} B C$.
$\therefore \angle E A C=\frac{1}{2} \angle B A C=\frac{\alpha}{2}$.
$\because \angle A C D$ 利 $\angle B A C$ 互.补,
$\therefore \angle A C D=180^{\circ}-\angle B A C=180^{\circ}-\alpha$.
$\because A C=C D$,
$\therefore \angle C A D=\angle C D A=\frac{\alpha}{2}$.
$\therefore \angle C A D=\angle E A C$.
$\therefore A C$ 为 $\angle E A H$ 的角平分线.
又 $\because C H \perp A D, A E \perp B C$,
$\therefore C H=C E$.
$\because C E=\frac{1}{2} B C$,
$\therefore C H=\frac{1}{2} B C$.
(3) $\angle A C D=\angle B A C$ 或 $\angle A C D+\angle B A C=180^{\circ}$.

①点击首页查看更多试卷和试题 , 点击查看本题所在试卷
② 下载本题Word版或下载本题PDF版点击赞助本站

关闭