两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图 形称为“手拉手”图形.
(1)问题发现:
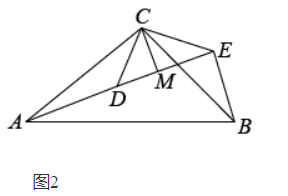
如图1,若 $\triangle A B C$ 和 $\triangle A D E$ 是顶角相等的等腰三角形, $B C , D E$ 分别是底边.求证: $B D=C E$ ;
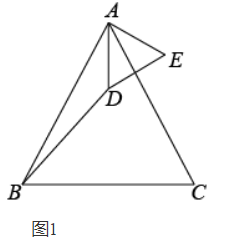
(2)解决问题: 如图2,若 $\triangle A C B$ 和 $\triangle D C E$ 均为等腰直角三角形, $\angle A C B=\angle D C E=90^{\circ}$ ,点 $A , D , E$ 在同一条直线上,CM为 $\triangle D C E$ 中 $D E$ 边上的高,连接 $B E$ ,请判断 $\angle A E B$ 的度数及线段 $C M , A E , B E$ 之间的数量关系并说明理由.