成都作为常住人口超 2000 万的超大城市, 注册青年志愿者人数超 114 万, 志愿服务时长超 268 万小时. 2022 年 6 月, 成都 22 个市级部门联合启动了 2022 年成都市青年志愿服务项目大赛, 项目大赛申报期间, 共收到 331 个主体的 416 个志愿服务项目, 覆盖文明实践、社区治理与邻里 守望、环境保护等 13 大领域. 已知某领域共有 50 支志愿队伍申报, 主管部门组织专家对志愿者 申报队伍进行评审打分, 并将专家评分(单位: 分) 分成 6 组: $[40,50),[50,60), \cdots,[90,100]$, 得 到如图所示的频率分布直方图.

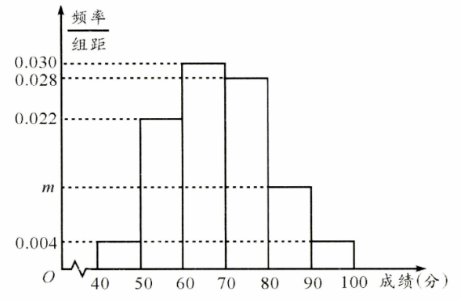
(I) 求图中 $m$ 的值;
(II) 已知评分在 $[85,100]$ 的队伍有 4 支, 若从评分在 [80, 90) 的队伍中任选 两支队伍, 求这两支队伍至少有一支队 伍评分不低于 85 分的概率.