返回 导出PDF     导出Word     在线讲解     加入试卷
题号:3921    题型:解答题    来源:2022年西藏中考数学真题答案 入库日期 2023/1/7 14:15:28
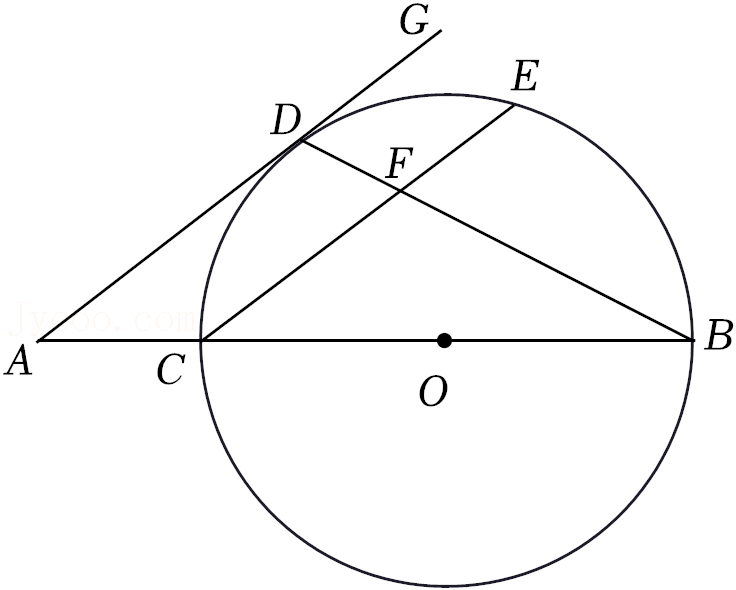
如图, 已知 $B C$ 为 $\odot O$ 的直径, 点 $D$ 为 $\widehat{C E}$ 的中点, 过点 $D$ 作 $\mathrm{DG} / / \mathrm{CE}$, 交 $\mathrm{BC}$ 的延长线于点 $\mathrm{A}$, 连接 $\mathrm{BD}$, 交 $\mathrm{CE}$ 于点 $\mathrm{F}$.
(1) 求证: $\mathrm{AD}$ 是 $\odot O$ 的切线;
(2) 若 $\mathrm{EF}=3, \mathrm{CF}=5, \tan \angle \mathrm{GDB}=2$, 求 $\mathrm{AC}$ 的长.
【答案】 26.(1)证明：如图，连接$OD$，$BE$

$\because$ 点 $\mathrm{D}$ 为 $\widehat{C E}$ 的中点,
$$
\therefore \widehat{C D}=\widehat{\mathrm{ED}} \text {, }
$$
$$
\therefore \angle \mathrm{CBD}=\angle \mathrm{EBD} \text {, }
$$
$$
\because \mathrm{OB}=\mathrm{OD} \text {, }
$$
$$
\therefore \angle \mathrm{ODB}=\angle \mathrm{CBD} \text {, }
$$
$$
\therefore \angle \mathrm{ODB}=\angle \mathrm{EBD} \text {, }
$$
$$
\therefore \mathrm{OD} / / \mathrm{BE} \text {, }
$$
$\because B C$ 为 $\odot O$ 的直径,
$$
\therefore \angle \mathrm{CEB}=90^{\circ} \text {, }
$$

$$
\begin{aligned}
& \therefore \mathrm{CE} \perp \mathrm{BE}, \\
& \therefore \mathrm{OD} \perp \mathrm{CE}, \\
& \because \mathrm{AD} / / \mathrm{CE}, \\
& \therefore \mathrm{AD} \perp \mathrm{OD}, \\
& \because \mathrm{OD} \text { 是 } \odot \mathrm{O} \text { 的半径, } \\
& \therefore \mathrm{AD} \text { 是 } \odot \mathrm{O} \text { 的切线; }
\end{aligned}
$$


(2) 解: $\because \mathrm{DG} / / \mathrm{CE}$,
$$
\begin{aligned}
& \therefore \angle \mathrm{BFE}=\angle \mathrm{GDB}, \angle \mathrm{A}=\angle \mathrm{ECB}, \\
& \because \tan \angle \mathrm{GDB}=2, \\
& \therefore \tan \angle \mathrm{BFE}=2, \\
& \text { 在 } \mathrm{Rt} \triangle \mathrm{BEF} \text { 中, } \mathrm{EF}=3, \tan \angle \mathrm{BFE}=\frac{\mathrm{BE}}{\mathrm{EF}}, \\
& \therefore \mathrm{BE}=6, \\
& \because \mathrm{EF}=3, \mathrm{CF}=5, \\
& \therefore \mathrm{CE}=\mathrm{EF}+\mathrm{CF}=8, \\
& \therefore \mathrm{BC}=\sqrt{\mathrm{CE}}{ }^2+\mathrm{BE}^2=10, \\
& \therefore \mathrm{OD}=\mathrm{OC}=5, \\
& \text { 在 } \mathrm{Rt} \triangle \mathrm{BCE} \text { 中, } \sin \angle \mathrm{ECB}=\frac{\mathrm{BE}}{\mathrm{BC}}=\frac{6}{10}=\frac{3}{5}, \\
& \therefore \sin \mathrm{A}=\sin \angle \mathrm{ECB}=\frac{3}{5}, \\
& \text { 在 } \mathrm{Rt} \triangle \mathrm{AOD} \text { 中, } \sin \mathrm{A}=\frac{\mathrm{OD}}{\mathrm{OA}}=\frac{3}{5}, \mathrm{OD}=5, \\
& \therefore \mathrm{OA}=\frac{25}{3}, \\
& \therefore \mathrm{AC}=\mathrm{OA}-\mathrm{OC}=\frac{10}{3} .
\end{aligned}
$$

系统推荐
© 科数网
电子教材      试题索引      数学公式
科数网为您提供初中数学题库、高中数学题库、大学数学题库。