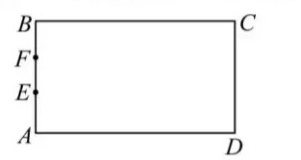
大连市2022～2023学年第一学期期末考试高二数学-Kmath科数- 中考、高考、考验数学题库

在某地举办的智能 $\mathrm{AI}$ 大赛中, 主办方设计了一个矩形场地 $A B C D$ (如图), $A B$ 的长为 9 米, $A D$ 的长为 18 米. 在 $A B$ 边上距离 $A$ 点 6 米的 $F$ 处有一只电子狗, 在距离 $A$ 点 3 米的 $E$ 处放置一个机器人. 电子狗的运动速度是机器人运动速度的两倍, 如果同时出发, 机器人比电子狗早到达或同时到达某点 (电子狗和机器人沿各自的直线方向到达某点), 那么电子狗将被机器人捕获, 电子狗失败, 这点叫失败点.
(1) 判断点 $A$ 是否为失败点 (不用说明理由);
（2）求在这个矩形场地内电子狗失败的区域面积 $S$;
(3) 若 $P$ 为矩形场地 $A D$ 边上的一动点, 当电子狗在线段 $F P$ 上都能逃脱时, 求 $\frac{|A P|}{|A D|}$ 的取值范围.