自 2019 年 1 月 1 日起, 对个人所得税起征点和税率进行调整。调整如 下: 纳税人的工资、薪金所得, 以每月全部收入额减去 5000 元后的余额为应纳税所得额。 依照个人所得税税率表, 调整前后的计算方法如表:
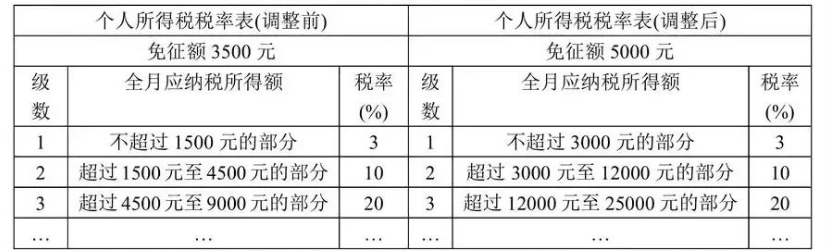
(1) 假如李先生某月的工资、薪金等所得税前收入总和不高于 8000 元, 记 $x$ 表示总收入, $y$ 表示应纳的税, 试分别求出调整前和调整后 $y$ 关于 $x$ 的函数表达式;
(2) 某税务部门在李先生所在公司利用分层抽样方法抽取某月 100 个不同层次员工的税前 收入, 并制成下面的频数分布表:

先从收入在 $[3000,5000)$ 及 $[5000,7000)$ 的人群中按分层抽样抽取 7 人, 再从中选 2 人作为新纳税法知识宣讲员, 求选中的 2 人收入都在 $[3000,5000)$ 的概率;